Determine the magnitude of the magnetic field.

[NasuSama]

Homework Statement

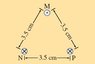
Three long parallel wires are 3.5 cm from one another. (Looking along them, they are at three corners of an equilateral triangle.) The current in each wire is 8.00 A, but its direction in wire M is opposite to that in wires N and P. Determine the magnitude of the magnetic field midway between points M and N.

Homework Equations

$B = \dfrac{\mu_0 I}{2\pi r}$

The Attempt at a Solution

First, I compute the field due points M and N, which is

$B_{MN} = \dfrac{2\mu_0 I}{\pi d}$

Then, the field due point P is

$B_P = \dfrac{mu_0 I}{\pi d\sqrt{3}}$

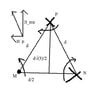
Working component wise, I obtain:

$B_x = B_{MN}\cos(30) + B_P\cos(60) = \dfrac{7}{2\sqrt{3}}\dfrac{\mu_0 I}{\pi d}$
$B_y = -B_{MN}\sin(30) + B_P\sin(60) = -\dfrac{\mu_0 I}{2\pi d}$

So we have

$B = \sqrt{(B_x)^2 + (B_y)^2} \approx 9.52 \times 10^{-5}$

But the answer is wrong.

 

[TSny]

Hello, NasuSama.

Check to see if you got the correct distance for $r$ for wire $P$. [Nevermind, I think you got it right!]

It looks to me that some of your trig functions are incorrect in finding the x and y components.

You might consider rotating the whole system so that M and N are at the base of the triangle.

 

[NasuSama]

I am not sure if rotating the system works.

Other than that, I edit my trig functions since I found they are incorrect by typos.

 

[TSny]

If you don't want to reorient the system, then let your x-axis pass through wires M and N and the y-axis pass through P and the midpoint of the line segment MN.

 

[NasuSama]

I got it!

(1) Turn the system 120$^{\circ}$ counterclockwise to get the diagram that looks like the one I uploaded.

(2) Using the 30-60-90 triangle postulate and the magnetic field formula, we get

$B_{MN} = 2B_{M}$
$= 2\dfrac{\mu_0 I}{2\pi \left(\frac{d}{2} \right)} = \dfrac{2\mu_0 I}{\pi d}$

$B_{P} = \dfrac{\mu_0 I}{2\pi \left(\frac{d\sqrt{3}}{2} \right)} = \dfrac{\mu_0 I}{\pi\sqrt{3}d}$

(3) Thus, by the Pythagorean Theorem, we have

$\sqrt{(B_{MN})^2 + (B_{P})^2} \approx 1.90 \times 10^{-4}$

 

[TSny]

Looks good!