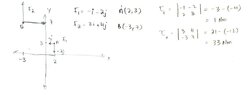Determine the point of application of a resultant force

[SumDood_]

Homework Statement

Given two Forces and their position vectors, find the resultant force and the point of application of the resultant Force.

Relevant Equations

moment = Force * distance

I am struggling with part b of the question attached in the screenshot. For part a, I simply add the components of the given forces.
I tried calculating the moments using vector cross multiplication, but I don't know what to do after that or even if that step is useful.

 

[BvU]

but I don't know what to do

a. Did you make a sketch ?

I tried calculating the moments

b. Please post your working -- and why you think this is useful

c. Post a typed problem statement, not a screenshot. See rules and guidelines

$\$

 

[BvU]

By the way, I agree with your ${\bf F} = \left (2{\bf \hat\imath}+ 2{\bf \hat\jmath}\right )\$ N.

 

[SumDood_]

a. Did you make a sketch ?
b. Please post your working -- and why you think this is useful

I did make a sketch now and attached my working. I calculated the moments because that is the material I am taking at the moment in class. I realized that the question does not mention that the system is in equilibrium, which is what I have used in previous questions.

 

[BvU]

Okay! No beauty prizes, but that's not the intention anyway. So you found (I hope) the $\bf F$ total and you found $\vec\tau_1 = -1\; {\bf \hat k} \$ Nm and $\vec\tau_2 = -33 \;{\bf \hat k} \$ Nm. Useful, because the resultant force and torque must both be the same.

I assume you found ${\bf F} = \left (2{\bf \hat\imath}+ 2{\bf \hat\jmath}\right )\$

So how did you (?) find that

?

the question does not mention that the system is in equilibrium

There is no system in this case. It's just the addition of two forces: a mathematical exercise.

$\$

 

[BvU]

Ah, I see. You didn't find: the screen shot is from the solutions manual.
No wonder I agreed...

So at this point you have a total $\vec F$ and a total $\vec \tau$ and I think your question boils down to "how do I find an x- and a y-coordinate for "the point where the resultant acts".
Am I right ?

$\$

 

[SumDood_]

Okay! No beauty prizes, but that's not the intention anyway. So you found (I hope) the $\bf F$ total and you found $\vec\tau_1 = -1\; {\bf \hat k} \$ Nm and $\vec\tau_2 = -33 \;{\bf \hat k} \$ Nm. Useful, because the resultant force and torque must both be the same.

I assume you found ${\bf F} = \left (2{\bf \hat\imath}+ 2{\bf \hat\jmath}\right )\$

So how did you (?) find that
View attachment 320129 ?There is no system in this case. It's just the addition of two forces: a mathematical exercise.

$\$

Thank you for the explanation! These are practice questions and I have the solutions for them. Why are your moments negative? From my working, they should be positive. Can you please explain that? From what I have read online, the cross multiplication of two dimensions generates an output that is on the third dimension which you have specified in your working, but why is it negative?

I'm also struggling with this:

Useful, because the resultant force and torque must both be the same.

Why must they both be the same?

 

[SumDood_]

I think your question boils down to "how do I find an x- and a y-coordinate for "the point where the resultant acts".
Am I right ?

$\$

Yes!

 

[BvU]

Why are your moments negative?

comes out as a result of

vector cross multiplication

I learned $\vec \tau = \vec r\times\vec F$ and I learned $$\vec a\times \vec b=\begin{vmatrix}\hat\imath&\hat\jmath&\hat k\\
a_x&a_y&a_z\\b_x&b_y&b_z\end{vmatrix}$$

And (for me) the sketch is a confirmation of the negative sign of the results: both forces turn clockwise, i.e. negative sense.

Why must they both be the same?

So that you have a single resulting force that does the same as the two forces combined

how do I find an x- and a y-coordinate for "the point where the resultant acts"

Vector sum of forces is ${\bf F} = \left (2{\bf \hat\imath}+ 2{\bf \hat\jmath}\right )\$
Sum of torques is $\vec\bf \tau = -34 \;{\bf \hat k} \$Nm.

From $\vec \tau = \vec r\times\vec F$ we get for a point $\vec r$ of action:$\tau_z = r_x F_y - r_y F_x$.
One equation in two unknowns (do you understand why there is one degree of freedom left over ?).

so we can finish the exercise by picking any two terms from the boxes that satisfy this condition...

$\$

 

[SumDood_]

comes out as a result of

I learned $\vec \tau = \vec r\times\vec F$ and I learned $$\vec a\times \vec b=\begin{vmatrix}\hat\imath&\hat\jmath&\hat k\\
a_x&a_y&a_z\\b_x&b_y&b_z\end{vmatrix}$$

And (for me) the sketch is a confirmation of the negative sign of the results: both forces turn clockwise, i.e. negative sense.So that you have a single resulting force that does the same as the two forces combinedVector sum of forces is ${\bf F} = \left (2{\bf \hat\imath}+ 2{\bf \hat\jmath}\right )\$
Sum of torques is $\vec\bf \tau = -34 \;{\bf \hat k} \$Nm.

From $\vec \tau = \vec r\times\vec F$ we get for a point $\vec r$ of action:$\tau_z = r_x F_y - r_y F_x$.
One equation in two unknowns (do you understand why there is one degree of freedom left over ?).

so we can finish the exercise by picking any two terms from the boxes that satisfy this condition...

$\$

Understood, thank you for your help!

 

[BvU]

In summary: a force does not have a point of action, but a line of action.

$\$