jaychay
- 58
- 0
Given that f is the function on (−∞, ∞) and the graph is the derivative of f
1.) Find the critical point on the graph ?
2.) Find the interval of the increasing function on the graph ?
3.) Find the interval of the decreasing function on the graph ?
4.) Find the point which is the absolute maximum on the graph ?
5.) Find the point which is the absolute minimum on the graph ?
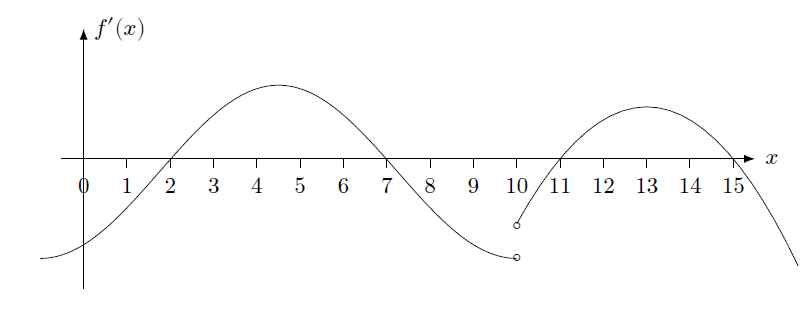
1.) Find the critical point on the graph ?
2.) Find the interval of the increasing function on the graph ?
3.) Find the interval of the decreasing function on the graph ?
4.) Find the point which is the absolute maximum on the graph ?
5.) Find the point which is the absolute minimum on the graph ?