Determine the total charge on the surface?

[nuagerose]

Homework Statement

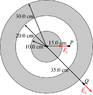
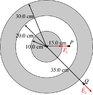
A hollow metal sphere has inner and outer radii of 20.0 cm and 30.0 cm, respectively. As shown in the figure, a solid metal sphere of radius 10.0 cm is located at the center of the hollow sphere. The electric field at a point P, a distance of 15.0 cm from the center, is found to be E1 = 1.53·104 N/C, directed radially inward. At point Q, a distance of 35.0 cm from the center, the electric field is found to be E2 = 1.53·104 N/C, directed radially outward.

Image of the problem: http://postimg.org/image/6cnneik69/

a) Determine the total charge on the surface of the inner sphere.
b) Determine the total charge on the surface of the inner surface of the hollow sphere.
c) Determine the total charge on the surface of the outer surface of the hollow sphere.

Homework Equations

∫∫$\vec{E}$ * $\vec{dA}$ = $\frac{q_{enc}}{E_{0}}$

The Attempt at a Solution

For part (a), I believe that the charge on the inner sphere from point P would be negative, since it is directed radially inward, while the charge on the inner sphere from point Q would be positive.
If I plug in the values into the equation above, then add them together, would I arrive at the correct answer?

I am still working on part (b) and (c), but want to make sure that I've set up part (a) correctly first.

 

[Enigman]

Use the direct link of image and put it in
[/IMG} tags replacing } with ]
[ATTACH=full]163767[/ATTACH]
Or attach it as an attachment.

 

[Enigman]

For part (a), I believe that the charge on the inner sphere from point P would be negative, since it is directed radially inward, while the charge on the inner sphere from point Q would be positive.
If I plug in the values into the equation above, then add them together, would I arrive at the correct answer?

Charge of inner sphere doesn't change with respect to different points. So 'charge on sphere from P' this statement is wrong. It is only electric field that changes.
Gauss law gives total charge enclosed by a surface. So for a spherical gaussian surface concentric with inner sphere and radius 15 cm i.e. passing through p shall enclose what charge?

 

[nuagerose]

Charge of inner sphere doesn't change with respect to different points. So 'charge on sphere from P' this statement is wrong. It is only electric field that changes.
Gauss law gives total charge enclosed by a surface. So for a spherical gaussian surface concentric with inner sphere and radius 15 cm i.e. passing through p shall enclose what charge?

For the outer spherical shell, would it enclose the charge of the inner sphere?

Also, given your explanation, I can then use the known electric field value at point P to calculate the charge of the inner sphere? From there, how do I work toward the charges on the inner and outer surfaces of the outer shell? I think that the inner surface of the outer shell would be the same as the charge of the inner sphere, correct?

 

[Enigman]

For the outer spherical shell, would it enclose the charge of the inner sphere?

Yep.

Also, given your explanation, I can then use the known electric field value at point P to calculate the charge of the inner sphere?

Yep.

From there, how do I work toward the charges on the inner and outer surfaces of the outer shell? I think that the inner surface of the outer shell would be the same as the charge of the inner sphere, correct?

Yeah, but you will need to prove that.Oh, and welcome to PF!
What's your favourite fish?