Determine the unknown angle (using the sine law)

In summary, the sine law, also known as the law of sines, is a trigonometric equation that can be used to determine the measure of an unknown angle in a triangle when the lengths of two sides and the measure of their included angle are known. It should be used when dealing with a triangle that has at least one known angle and its opposite side, and can be used for all types of triangles. The steps for using the sine law include identifying the triangle, setting up a proportion, and checking the answer. However, there are limitations and restrictions when using the sine law, such as the triangle must be a standard triangle and there must be enough known values for the law to be used.
  • #1
eleventhxhour
74
0
View attachment 2479

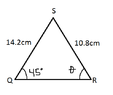
So using the sine law, I found that Θ = 68 degrees. And the I found that the other possibility of Θ would be 112 degrees (180 - 68 = 112). However, the textbook says that the answers are Θ = 68 and Θ = 23. What did I do wrong?

Thanks.
 

Attachments

  • 4b.png
    4b.png
    3 KB · Views: 43
Mathematics news on Phys.org
  • #2
I agree with your result, rounded to the nearest degree. You did everything correctly. :D
 
  • #3
MarkFL said:
I agree with your result, rounded to the nearest degree. You did everything correctly. :D

Alright, thanks! (:
 

Related to Determine the unknown angle (using the sine law)

1. What is the sine law and how does it relate to determining unknown angles?

The sine law, also known as the law of sines, is a trigonometric equation that relates the angles and sides of a triangle. It states that the ratio of the length of a side to the sine of its opposite angle is constant for all sides and angles in a triangle. This law can be used to determine the measure of an unknown angle in a triangle when the lengths of two sides and the measure of their included angle are known.

2. When should the sine law be used to determine unknown angles?

The sine law should be used when dealing with a triangle that has at least one known angle and its opposite side, as well as the length of another side. This can be used to solve for the measure of the remaining angles in the triangle.

3. What are the steps for using the sine law to determine an unknown angle?

The first step is to identify the triangle and label the known and unknown angles and sides. Then, use the sine law equation (a/sinA = b/sinB = c/sinC) to set up a proportion and solve for the unknown angle. Make sure to use the appropriate units (degrees or radians) for the angles and sides. Finally, check your answer by plugging it back into the equation to ensure it satisfies the proportion.

4. Can the sine law be used for all types of triangles?

Yes, the sine law can be used for all types of triangles, including acute, right, and obtuse triangles. However, it is important to note that the law may not always yield a unique solution for all types of triangles. In some cases, there may be multiple possible solutions or the triangle may not exist at all.

5. Are there any limitations or restrictions when using the sine law to determine unknown angles?

Yes, there are some limitations and restrictions when using the sine law. First, the triangle must be a standard triangle, meaning that the given information must be for a single triangle and not a combination of multiple triangles. Additionally, the sine law can only be used to solve for an unknown angle if the given information is sufficient. If there are not enough known values, the law cannot be used. Lastly, the sine law may not yield a unique solution for certain triangles, as mentioned in the previous question.

Similar threads

A Explicit example of two complex numbers for double cover U(1) of SO(2) for a specified angle
    • General Math
Replies
2
Views
520
B Calculating the perfect tennis shot using vectors
    • General Math
Replies
2
Views
1K
I Can the same argument be used for both radians and degrees in the sine function?
    • General Math
Replies
3
Views
843
Finding the angle between two vectors
    • Precalculus Mathematics Homework Help
Replies
2
Views
671
Angle of Depression Help: Using the Sine Rule to Solve for Unknown Angles
    • Introductory Physics Homework Help
Replies
5
Views
1K
MHB Where Did I Go Wrong in Calculating the Value of x in These Triangle Problems?
    • General Math
Replies
4
Views
2K
Mistake in Exercises for the Feynman Lectures?
    • Introductory Physics Homework Help
Replies
2
Views
342
I Why is it important to convert angle units when using trigonometric functions?
    • General Math
Replies
8
Views
1K
I Dimension of an Angle: Clarifying the SI Standard
    • General Math
Replies
1
Views
1K
For a Pendulum: Knowing Acceleration Find Maximum Angle
    • Introductory Physics Homework Help
Replies
26
Views
2K

Hot Threads

Recent Insights

Back
Top