Determine the velocity of two balls after the first collides with a lever

[leafy]

Homework Statement

Find the final velocity of B1 and B2 right after collision

Relevant Equations

E1=E2

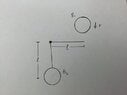
In the figure below Ball 2(B2) is hanging and attached to a square lever. B1 drop from gravity and hit the lever as shown. Calculate velocity of B1 and B2 with gravity influence right after collision. The mass of B1 and B2 is identical.

Using energy equation E1=E2, therefore VB2 final = VB1 initial, VB1 final= 0 Right after collision. But this is without gravity. How can I include gravity?

 

[haruspex]

There must have been more information. Were you given the velocity of B1 just before it hits the lever? If not, what?
The velocities immediately after the collision are not affected by gravity. Acceleration takes time to alter velocities.

How do you know energy is conserved?
Please state the whole question exactly as given to you.

 

[leafy]

This is a problem given by a friend. B1 could be any velocity. During the duration of collision gravity is a net force. Isn’t this net force contribute to the increase in velocity? I can only start with conservation of energy, but it only work if this was in space without gravity.

 

[haruspex]

B1 could be any velocity.

Sure, but you need to know what variables are allowed in the answer. If the question says the speed of B1 immediately before impact is $v_1$, say, then you know $v_1$ is allowed in the answer; but if told B1 was dropped from height h then you would use that.

During the duration of collision gravity is a net force.

Yes, but how long does the collision last? If not told then you should take it as instantaneous, and since the change in velocity is acceleration x time, acceleration has no effect.

I can only start with conservation of energy

In general, it is not conserved in a collision, so questions would usually specify an elastic collision if that is what you are to use. Otherwise it should provide further info, such as the velocity of one ball after the collision.

 

[leafy]

Oh I see. You’re right.

the VB1 right before collision is what I meant. The collision is perfect elastic. Duration of collision is any non zero t we choose to make sense. Thanks.

I think we want to see what happens during collision.

 

[leafy]

I come up with a solution, but it doesn’t make any sense. Gravity force is mg and both masses are stuck together via the lever during collision, therefore the acceleration is halve. So after collision:

VB1= 1/2g x t
VB2= VB1(before collision) + 1/2g x t

This violate conservation of energy since the change in B1 height during collision cannot account for the extra energy.

 

[haruspex]

both masses are stuck together via the lever during collision

Then energy will not be conserved. That constitutes coalescence.
For finding the velocity immediately after, use conservation of angular momentum instead. Do you see how?
Gravity will still not affect the velocity immediately after, just the acceleration.

 

[leafy]

I don’t mean stuck together as inelastic collision. I mean stuck together as temporary store energy and exchange energy by deformation, like a spring on microscopic level. Gravity only affect during collision.

 

[haruspex]

I come up with a solution, but it doesn’t make any sense. Gravity force is mg and both masses are stuck together via the lever (only) during collision, therefore the acceleration is halve. So after collision:

VB1= 1/2g x t
VB2= VB1(before collision) + 1/2g x t

This violate conservation of energy since the change in B1 height during collision cannot account for the extra energy.

How do you arrive at those two equations? If B1 is now falling from rest and beforehand it had a nonzero velocity then it is not keeping up with B2, so why are they sharing in the acceleration due to gravity?
If you want to model it as a spring, do it properly or you may deceive yourself.

 

[leafy]

Let just say right before collision VB1= 10m/s. It hits the lever for .3 seconds. If there is no gravity involve, B1 would come to a complete stop after collision and VB2 would be 10m/s.

So how does gravity affect those numbers because it play a role in those .3 seconds.

 

[haruspex]

Let just say right before collision VB1= 10m/s. It hits the lever for .3 seconds. If there is no gravity involve, B1 would come to a complete stop after collision and VB2 would be 10m/s.

So how does gravity affect those numbers because it play a role in those .3 seconds.

Not enough detail.
You are supposing some force or torque acts between the balls, mediated by the lever, to share the gained KE. But if the forces (torques) are equal and opposite and the gap between them is increasing then that force (torque) is doing net work on the system.
You need to specify exactly how this connection works.

 

[leafy]

We can take the lever away and replace it with simple collision as shown. Would this be the same?

 

[haruspex]

We can take the lever away and replace it with simple collision as shown. Would this be the same?

Yes.

 

[leafy]

Okay, a net force is applied for the duration of collision, say .3 second. This would simulate gravity. Yes?

 

[haruspex]

Okay, a net force is applied for the duration of collision, say .3 second. This would simulate gravity. Yes?

Sure. Where is the force applied? How does the force between the balls behave, like a spring?

 

[leafy]

The force applied in the direction of the moving ball of course. You can say the force between the ball behaves like a spring, but the applied forced only see them as a single object. So after collision

right ball speed= 1/2 a x .3 seconds
left ball speed = v + 1/2 a x .3 seconds

 

[haruspex]

The force applied in the direction of the moving ball of course. You can say the force between the ball behaves like a spring, but the applied forced only see them as a single object. So after collision

right ball speed= 1/2 a x .3 seconds
left ball speed = v + 1/2 a x .3 seconds

I meant is it applied only to one ball and in the direction towards the other ball? I assume so.

Your equations above need to be justified by an actual mechanism. If the force between them is like a spring then they will not generally have the same acceleration.

If their displacements from where they were at contact are $x_L, x_R$ and the force per unit mass between them is C(t) then
$\ddot x_R=F-C$
$\ddot x_L=C$
$C=k(x_R-x_L)$
This is clearly SHM plus a constant acceleration of the system. The COM will move at speed $\frac{v+Ft}2$, so the solution is of the form
$x_R=\frac{2vt+Ft^2}4+A\sin(\omega t)$, $x_L=\frac{2vt+Ft^2}4-A\sin(\omega t)$, where $\omega^2=2k, A=\frac v{2\omega}$.
This applies until contact is lost ($x_R=x_L$).

 

[leafy]

You lost me on the math but I agree the two mass do not generally have the same acceleration, but the spring modeled force is much greater than the applied force so we can assumed they instantly come to the same acceleration.

right ball center of mass speed for each interval starting with 10 would be:
10,9,8,7,6,5,4,3,2,1
left ball center of mass speed:
1,2,3,4,5,6,7,8,9,10

the applied force add speed to both balls In addition.

 

[haruspex]

You lost me on the math but I agree the two mass do not generally have the same acceleration, but the spring modeled force is much greater than the applied force so we can assumed they instantly come to the same acceleration.

right ball center of mass speed for each interval starting with 10 would be:
10,9,8,7,6,5,4,3,2,1
left ball center of mass speed:
1,2,3,4,5,6,7,8,9,10

the applied force add speed to both balls In addition.

If you do not model it realistically you may very well end up with an apparent conservation violation.

 

[leafy]

Yes, to keep it simple both masses are identical in mass and stiffness. I think this is something since we always neglect what happens during collision.

 

[haruspex]

Yes, to keep it simple both masses are identical in mass and stiffness. I think this is something since we always neglect what happens during collision.

My point is that the pattern you propose in post #18 is invalid. For energy conservation, the sum of squares of the velocities should be constant. Your sequence goes 101, 85, 73, 65...

 

[leafy]

But I used momentum conservation. One ball decrease in speed will be the other ball gained in speed.

 

[haruspex]

But I used momentum conservation. One ball decrease in speed will be the other ball gained in speed.

yes, sorry, I forgot about the elastic potential energy. You can assume that makes up the difference.

 

[leafy]

Yeah, I was waiting to see if you catch that. Lol