Determine vertical velocity vector on sloped surface

[hjam24]

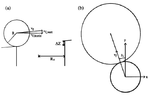
A golf is launched at a speed v,f and launch angle, β,f. The slope of the green is equal to φ. At some point the ball is located on the rim of a hole. The side view (a) and overhead view (b) looks as in the attached image.


According to the author of the [paper][2] "The Physics of Putting" the vertical velocity is given by

$$ v_{f,v} = v_f \cdot \cos(\beta) \cdot \sin(\phi) $$

The horizontal velocity is equal to:

$$ v_{f,h} = v_f \cdot (\cos^2(\beta_f) \cos^2(\phi) + \sin^2(\beta_f))^{1/2} $$

I understand the reasoning behind the vertical velocity component. Basically we have the hypotenuse, v,fy (v,f * cos(β,f)) and multiply this with sin(φ). Now we have the opposite. However, why is the author not following the same logic for the horizontal velocity and multiplying the hypotenuse with cos(φ)? Please show me how his formulation is derived.

My (unsuccessful) attempt:

Pythagorean theorem

$$ \sin^2(\phi) + \cos^2(\phi) = \frac {v_{f,h}^2 + v_{f_v}^2} {v_f^2} $$

$$ v_f^2 \cdot (\sin^2(\phi) + \cos^2(\phi)) = v_{f,h}^2 + v_{f_v}^2 $$

$$ v_{f,h}^2 = v_f^2 \cdot (\sin^2(\phi) + \cos^2(\phi)) - v_{f_v}^2 $$

Substitute vertical velocity according to author

$$ v_{f,h}^2 = v_f^2 \cdot (\sin^2(\phi) + \cos^2(\phi)) - (v_f\cos(\beta)\sin(\phi))^2 $$

v,f is v,fy

$$ v_{f,h}^2 = (v_f\cos(\beta))^2 \cdot (\sin^2(\phi) + \cos^2(\phi)) - (v_f\cos(\beta)\sin(\phi))^2 $$

$$ v_{f,h}^2 = v_f^2\cos^2(\beta) \cdot (\sin^2(\phi) + \cos^2(\phi)) - v_f^2\cos^2(\beta)\sin^2(\phi) $$

$$ v_{f,h}^2 = v_f^2\cos^2(\beta)\sin^2(\phi) + v_f^2\cos^2(\beta)\cos^2(\phi) - v_f^2\cos^2(\beta)\sin^2(\phi) $$

$$ v_{f,h}^2 = v_f^2\cos^2(\beta)\cos^2(\phi) $$

$$ v_{f,h}^2 = v_f^2\cos^2(\beta)\cos^2(\phi) $$

$$ v_{f,h} = v_f(\cos^2(\beta)\cos^2(\phi))^{1/2} $$

Let me know what I am doing wrong. Thanks in advance

[2]: http://www.puttingzone.com/Science/cjp-putting.pdf

 

[anuttarasammyak]

After getting the formula of $v_{f\ vertical}$, the author seems to have made use of Pythagoras relation
$$v_{f\ vertial}^2+v_{f\ horizontal}^2=v_f^2$$
So
$$v_{f\ horizontal}^2=v_f^2-v_{f\ vertial}^2$$

 

[vela]

You have to consider all three dimensions. Your logic applies to the y- and z- components, but it neglects the x-component. To see this, consider the case where $\phi=0$. Using your logic, you'd say $v_{f,v}=0$, as expected, but $v_{f,h}=v_f\cos\beta$. But if there's no vertical component, shouldn't $v_{f,h}=v_f$?

A straightforward way to see what's happening is to first consider the case where $\phi=0$. Then the components of the velocity will be
$$\mathbf v_f = -v_f \sin\beta\,\mathbf i + v_f \cos\beta\,\mathbf j + 0 \,\mathbf k.$$ Now add in the effect of the uphill slope, which mathematically is a rotation by an angle $\phi$ about the x-axis. The rotation will leave the x-component unchanged but will turn the y-component into a combination of y- and z- components.

 

[hjam24]

A golf ball is launched at a speed v and launch angle, β . At some point the ball is located on the rim of a hole. The view from above looks as follows:

Vector v can be expressed in two components, v_v and v_y:


$$v_y = v \cdot \cos(\beta)$$

and

$$v_x = v \cdot \sin(\beta)$$

If we look at the surface from a different angle, we see that the surface has a slope.
The slope of the green is equal to φ (along the y-axis).

v_v is perpendicular to the y-axis. As a result:

$$v_v = v \cdot \cos(\beta) \cdot \sin(\varphi)$$

Let's assume now there is no slope across the y-axis (φ=0), but there is a slope across the x-axis, θ.

Following the same logic v_v is perpendicular to the x-axis. As a result:

$$v_v = -1 \cdot v \cdot \sin(\beta) \cdot \sin(\theta)$$

What is the formula of v_v expressed in terms of both φ and θ? So, in the case that the surface is sloped/inclined across both the x- and y-axis?

[Moderator's note: moved from a technical forum.]

 

[berkeman]

A golf ball is launched at a speed v and launch angle, β . At some point the ball is located on the rim of a hole. The view from above looks as follows:

@hjam24 -- Why did you repost this question and show no work? Were the replies above to your original thread a couple weeks ago not helpful enough?

 

[hjam24]

@hjam24 -- Why did you repost this question and show no work? Were the replies above to your original thread a couple weeks ago not helpful enough?

Hi,

The previous question was with a singe slope across one axis, this question involves a slope across bot the x-axis and the y-axis. I believe the difference is large enough to open a new topic. I am sorry if I misjudged that

 

[berkeman]

Well the wording was so similar that it was hard to tell the difference.

What is the formula of v_v expressed in terms of both φ and θ? So, in the case that the surface is sloped/inclined across both the x- and y-axis?

Please show your work on this, and you should continue to get good help. Thank you.

 

[haruspex]

why is the author not following the same logic for the horizontal velocity and multiplying the hypotenuse with cos(φ)?

In the direction of the ball, the slope is not $\phi$.

$$ v_{f,h}^2 = v_f^2 \cdot (\sin^2(\phi) + \cos^2(\phi)) - (v_f\cos(\beta)\sin(\phi))^2 $$

v,f is v,fy

$$ v_{f,h}^2 = (v_f\cos(\beta))^2 \cdot (\sin^2(\phi) + \cos^2(\phi)) - (v_f\cos(\beta)\sin(\phi))^2$$

I don’t understand what you did there. You seem to have just multiplied a term by $\cos^2(\beta)$.

 

[Lnewqban]

A golf ball is launched at a speed v and launch angle, β . At some point the ball is located on the rim of a hole.

What is your question for the second case?
The vertical velocity vector is perpendicular to both top views, as well as to the axis that is not tilted (or remains horizontal).

 

[vela]

It would be nice if the OP actually replied to the posts so we know if he understood what was said or not.