Determing components of a projectile from ferquency

[centripitacal]

I have been given a graph with 5 squares along the x-axis and 8 squares along the y-axis, with each square 10x10 cm.

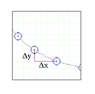
The graph shows the motion of a projectile entering the graph after accelerating down a curved ramp and up again. The graph is a stroboscopic photograph of the projectile.

The question wants me to find the horizontal component of the projectile as it leaves the track.

Homework Equations

I tells me the frequency of the stroboscope is 12.5 Hz and each square on the grid represents 10x10cm

The answer is 0.625ms

The Attempt at a Solution

I am baffled as to what to do. I know that frequency= lambda/s.

Also that I could label each square 0.1, 0.2 and so on but it still is not helping me how to work out the horizontal velocity component.

Any help please to point me in the right direction would be appreciated.

 

[gneill]

If the frequency of the strobe is 12.5 Hz, what is the time between flashes?

If you know the time between flashes then you also know the time between images of the projectile. Call it Δt. The grid allows you to measure the change in distance from image to image, in both the X and Y directions. Call them Δx and Δy.

How might you estimate the horizontal velocity of the projectile given Δx and Δt?