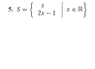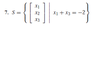Determining a Subspace: Problem and Conditions

[pyroknife]

The problem is attached. I need to determine if it's a subspace.
So it must satisfy 3 conditions:
1) 0 vector is in S
2) if U and V are in S then U+V is in S
3) if V is in S, then cV where c is a scalar is in S


For the 1st condition:
I said the 0 vector is not in S, but I'm not sure if I'm understanding it correctly. For this problem when we say the 0 vector is in S are we asking if we have x=0 does that give us the 0 vector?


Let's say we changed the bottom element to 2y-1 instead of 2x-1. And if x and y are in R.
For this case, the 0 vector would be in S right? We can have x=0 and y=1/2 which gives the 0 vector?

 

[pyroknife]

Another question I have is for another problem (I attached this in this post). My book is trying to prove that S is not closed under addition and scalar multiplication. I don't understand why it's necesasry to do that.
Can't you just look at it and see that if the 0 vector is in S, then that means x1=0 and x3=0, but x1+x3=0+0≠-2, which means the 0 vector isn't in S. What is the point of proving the more complicated steps?

 

[pyroknife]

Bump, anyone?