vwishndaetr
- 86
- 0
- TL;DR
- I am trying to determine the reactance of a circuit if I know the resistance, current, and voltage. I am speculating that current imbalances of parallel runs that are equal in resistance are caused by the differing reactance in the circuit.
I am trying to figure something out, but I am in the first step and just trying to get through my "thought experiment".
Let's say I have a 480V 60hz 3 phase supply feeding a circuit that comprises of nothing but the conductors themselves (effectively a shorted power supply). Consider the circuit below: power supply that has a couple parallel runs between the short and the supply.
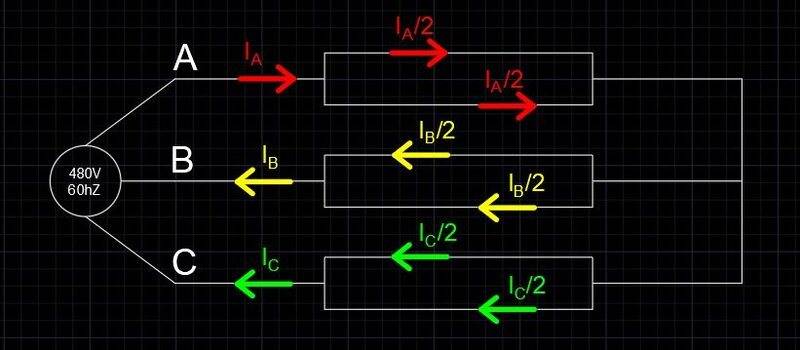
I want to figure out what self imposed reactance is being produced by the circuit. More specifically in the parallel runs.
Theoretically, in a perfect world the current in the parallel runs should be half the total current in say phase A (ultimately this will be broken down to 3 single phase circuits, but I wanted to show the whole picture here - so consider everything going forward is about phase A only). If one of the parallel runs draws more current than the other, and the resistance across the two parallel runs is equal, then is it safe to assume that I have some reactance that is creating the current imbalance between the parallel runs? After all, impedance comprises of resistance and reactance. Why else would I have an imbalance? With that being said can I determine what the reactance is if I know the voltage, across the parallel runs, the current in each, and the resistance of each?
I think I have formulas at my disposal to calculate this, but I want to know if my theory makes sense... My electrical knowledge is limited to being in the industry... formal education is mechanical in nature.
TIA for the help, came on here a bunch in my college days when I had other thing explained to me - figured this would be a great place to get some feedback on this.
Let's say I have a 480V 60hz 3 phase supply feeding a circuit that comprises of nothing but the conductors themselves (effectively a shorted power supply). Consider the circuit below: power supply that has a couple parallel runs between the short and the supply.
I want to figure out what self imposed reactance is being produced by the circuit. More specifically in the parallel runs.
Theoretically, in a perfect world the current in the parallel runs should be half the total current in say phase A (ultimately this will be broken down to 3 single phase circuits, but I wanted to show the whole picture here - so consider everything going forward is about phase A only). If one of the parallel runs draws more current than the other, and the resistance across the two parallel runs is equal, then is it safe to assume that I have some reactance that is creating the current imbalance between the parallel runs? After all, impedance comprises of resistance and reactance. Why else would I have an imbalance? With that being said can I determine what the reactance is if I know the voltage, across the parallel runs, the current in each, and the resistance of each?
I think I have formulas at my disposal to calculate this, but I want to know if my theory makes sense... My electrical knowledge is limited to being in the industry... formal education is mechanical in nature.
TIA for the help, came on here a bunch in my college days when I had other thing explained to me - figured this would be a great place to get some feedback on this.