Determining Max/Mins, Critical Points (Conceptual)

[jegues]

Homework Statement

I don't have a particular problem in mind, just trying to recap a method my professor quickly skimmed over for determining whether a point is a max or a min.

I had suggested that we use the second derivative test on our critical to determine whether it is a max or a min and go from there, but he had ranted and raved that he didn't like that method and that will only determine relative max/mins not absolute max/mins.

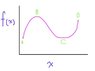
He drew me a picture like the figure attached. I can't remember exactly what he said but it went something like this, (Maybe if I mix some things up you guys can help me clarify)

You have some curve with endpoint A and D, and two critical points B and C. Now look at the values of those points evaluated for the given function and look at the limits around those points and you should be able to see if it's a max or a min.

Can someone further clarify/explain this for me, it's still kinda confusing. An example would probably help too!

Homework Equations

N/A.

The Attempt at a Solution

N/A.

 

[zhermes]

For the record, the second derivative test is the way to go, good call.
But he is correct that it only tells you if something is a local max or min. To find out if its a global max/min you have to compare with every value of the function (i.e. there is, in general, no easy way to do it).

I think maybe what he was going for, is if you know the values of the function at those four points (the two critical points, and the 2 end points), you can also figure it out (but that only works when you have well defined end points, and you know all of your critical points.
Anyway, out of those 4 points, one (or more) have to be the global max's/min's of the function. If there is one local maximum, and its value is larger than both end points, its a global maximum.

Moral of the story is: if you have a picture of the graph you can pick which one is the global max/min; otherwise use the second derivative test to find local max/mins.

 

[jegues]

For the record, the second derivative test is the way to go, good call.
But he is correct that it only tells you if something is a local max or min. To find out if its a global max/min you have to compare with every value of the function (i.e. there is, in general, no easy way to do it).

I think maybe what he was going for, is if you know the values of the function at those four points (the two critical points, and the 2 end points), you can also figure it out (but that only works when you have well defined end points, and you know all of your critical points.
Anyway, out of those 4 points, one (or more) have to be the global max's/min's of the function. If there is one local maximum, and its value is larger than both end points, its a global maximum.

Moral of the story is: if you have a picture of the graph you can pick which one is the global max/min; otherwise use the second derivative test to find local max/mins.

Even if you don't have explicitly defined end points you can just evaluate the limit as x goes to +/- infinity, no?

 

[zhermes]

Even if you don't have explicitly defined end points you can just evaluate the limit as x goes to +/- infinity, no?

If you know that there aren't any other extrema, then yes; but in general, no---you could simply have another maximum somewhere further along, while x still asymptotically approaches (e.g.) zero.