Determining stationary and mean-ergodicity

[ashah99]

Homework Statement

Please see problem below

Relevant Equations

Autocorrelation function R(m) = E(X_k*X_(k+m))

I am having difficulties setting up and characterizing stationary and ergodicity for a few random processes below. I need to determine whether the random process below is strict-sense stationary (SSS), whether it is wide-sense stationary (WSS), and whether it is ergodic in the mean. All help is much appreciated.

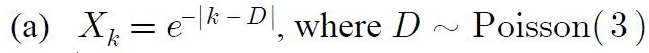
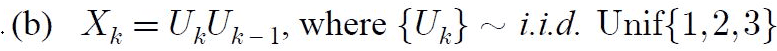Approach to (a) :
Since the Poisson RV includes a time duration in its PDF, then X_k would depend on time, so it is not WSS.
To test for SSS, I simply replace k with k - d , so X_(k-d) = e^-|k-d - D|, but since it is not WSS, then it would still dependent on time, so it is not SSS.
I'm not sure how to approach proving if the ensemble and time averages are the same or not. A time average is generally a RV and an ensemble average is generally a function of time. Any help appreciated.

As for (b)
The mean would be constant E(X_k) = (1/3)(1/3) = 1/9, but I'm not sure how to write out the autocorrelation function, but my hutch is that it's dependent of time, since it's equally likely to be 1, 2, or 3 -> random process is not WSS.
To test for SSS, a similar approach with a time delay as with part (a). I suspect the process is not SSS and depends on time k since {U_k} ~ i.i.d Unif(1,2,3)
I think that given the U_k, the ensemble and time average would both come out as 1/9, meaning that the process is mean-ergodic.

 

[Asim Riaz]

Approach to (c):The mean is constant E(X_k) = 0, and the autocorrelation function would be r_x(k) = E[X_k X_(k-d)] = 0, since the variance is 0. Therefore, the process is WSS and SSS.To prove ergodicity, the ensemble and time average would need to be equal. The ensemble average would be 0, but I'm not sure how to calculate the time average. Any help appreciated.