- #1
Amer
- 259
- 0
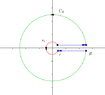
what is the suitable contour for the integral
$\displaystyle \int_0^{\infty} \dfrac{\log (x) }{x^2 +1 } dx $
and why ? or what is the method to determine a good one?
$\displaystyle \int_0^{\infty} \dfrac{\log (x) }{x^2 +1 } dx $
and why ? or what is the method to determine a good one?