Determining the horizontal asymptote

[chwala]

Homework Statement

see attached

Relevant Equations

rational functions

Consider,

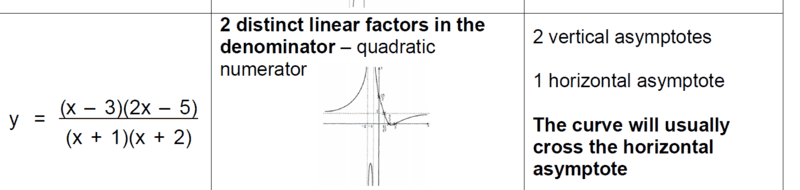
I am self-studying;

My interest is on the horizontal asymptote, now considering the degree of polynomial and leading coefficients, i have
$y=\dfrac{2}{1} =2$ Therefore $y=2$ is the horizontal asymptote.

The part that i do not seem to get is (i already checked this on desmos) why an asymptote can be regarded as such if it is crossing the curve. In my small understanding, i thought asymptote ought not to intersect any curve or line...
For vertical asymptote, that is straightforward, solving the denominator, shall give me $x=-1$ and $x=-2$.
Thanks

 

[chwala]

This is related to the original post;

What about the horizontal asymptote? $y=1$? Now considering the fact that asymptotes can cross curves.

 

[Orodruin]

An asymptote is about how a curve behaves at infinity, not how the behaviour looks in some intermediate range. It does not matter at all if it crosses the curve or not. All that is relevant is whether or not the curve approaches the asymptote at infinity.

This is related to the original post;

View attachment 343040

What about the horizontal asymptote? $y=1$? Now considering the fact that asymptotes can cross curves.

What about it?

 

[Orodruin]

Another example, here is the plot of $y(x) = \sin(x)/x^3$:

It has the asymptote $y = 0$ as $x\to \infty$, but crosses the asymptote an infinite number of times.

Edit: Function in orange, asymptote in blue.

 

[chwala]

An asymptote is about how a curve behaves at infinity, not how the behaviour looks in some intermediate range. It does not matter at all if it crosses the curve or not. All that is relevant is whether or not the curve approaches the asymptote at infinity.


What about it?

Noted, that is clear. I am now looking at how to determine the stationary points; either for local maximum or local minimum. To close this well, let me determine that and share ... considering the function in post $1$. I have

$y= \dfrac{(x-3)(2x-5)}{(x+1)(x+2)}$

Let the graph meet the horizontal line $y=k$

$k= \dfrac{(x-3)(2x-5)}{(x+1)(x+2)}$

$kx^2+3kx+2k=2x^2-11x+15$

$(k-2)x^2+(3k+11)x+2k-15≥0$

$(9k^2+66k+121)-4(2k^2-19k+30) ≥0$

$9k^2+66k+121-8k^2+76k-120 ≥0$

$k^2+142k+1 ≥0$


$k=-141.99 ⇒x= -1.441$ will give us local maximum

and $k=-0.007 ⇒ x= 2.755$ will give us local minimum.

Cheers @Orodruin ... most math concepts I teach myself. Of course with great support from Physics Forums! Bingo!

 

[Mark44]

Noted, that is clear. I am now looking at how to determine the stationary points; either for local maximum or local minimum. To close this well, let me determine that and share ... considering the function in post 1. I have
$y= \dfrac{(x-3)(2x-5)}{(x+1)(x+2)}$

Let the graph meet the horizontal line $y=k$
<snip>

Or you could find the derivative $\frac{dy}{dx}$ and see where it is zero. Maxima or minima can be found at places were a) the derivative is zero, or b)places where the derivative is undefined (as for example y = |x|), or c) endpoints of a possibly restricted domain of the original function.

 

[chwala]

Or you could find the derivative $\frac{dy}{dx}$ and see where it is zero. Maxima or minima can be found at places were a) the derivative is zero, or b)places where the derivative is undefined (as for example y = |x|), or c) endpoints of a possibly restricted domain of the original function.

That is correct, using derivative i have

$\dfrac{dy}{dx} = \dfrac{17x^2-22x-67}{(x+1)^2 (x+2)^2} =0$

$⇒17x^2-22x-67=0$

$x_1=-1.44$ and $x_2=2.74$ as shown in post $5$.