- #1
aaronfue
- 122
- 0
Homework Statement
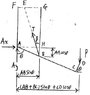
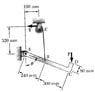
The position of the L-shaped rod shown is controlled by a cable attached at point B. Determine the angle, β, in terms of θ.
The Attempt at a Solution
From the FBD attached, I was able to get:
β = tan-1([itex]\frac{0.24sinθ - EF}{0.24cosθ+0.32}[/itex])
How can I determine what EF is? Is it possible to get an actual number? FG = 0.160
Attachments
Last edited: