kurt101
- 285
- 35
- TL;DR Summary
- How is a polarizer experiment where changes to the polarization state are restored by following the reverse process understood by different quantum mechanical interpretations?
If light at a known polarization goes through a beam splitting polarizer that changes the light's polarization and then goes through the reverse orientation of that polarizer it will exit with the same polarization that it entered with. See the following picture:
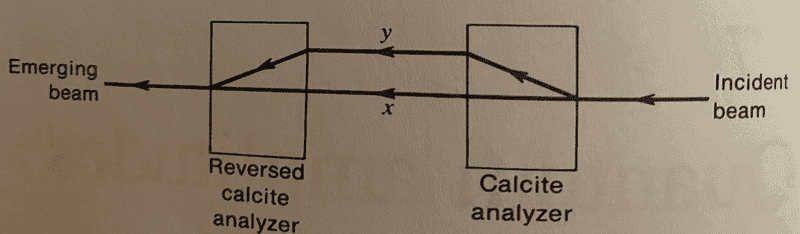
If the polarization state can be changed and then later changed back to its original state by following the reverse process, doesn't this imply these changes are deterministic?
How is this experiment understood by someone who supports the interpretation that our universe is fundamentally probabilistic?
If the polarization state can be changed and then later changed back to its original state by following the reverse process, doesn't this imply these changes are deterministic?
How is this experiment understood by someone who supports the interpretation that our universe is fundamentally probabilistic?