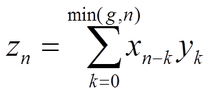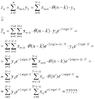DFT for convolution like operation.

[menahemkrief]

Let x,y be finite real valued sequences defined on 0...N-1 and let g be a non negative integer .

define
View attachment 2231
also on 0..N-1.

In addition, the DFT of y is known in closed form.
Is there a way to write z as some cyclic convolution, so that with the help of the convolution theorem z can be calculated in NLOG N istead of N^2?

Thank you

 

[Ackbach]

It would seem you can do that. First note that the unusual upper limit of your sum, arbitrarily cut off at $g$, poses no issue for this algorithm. Simply re-define the $x$ and $y$ sequences to include only the terms that show up in the convolution sum. I'm not sure that knowing the FFT of $y$ in advance will help you, since you really need to truncate the sequence, at least in general.

1. Take the FFT's of the re-defined $x$ and $y$. Complexity is $\mathcal{O}(n \, \log(n))$.
2. Multiply the two transformed sequences point-wise. Complexity is $\mathcal{O}(n)$.
3. Take the inverse FFT of the result. Complexity is $\mathcal{O}(n \, \log(n))$.

 

[menahemkrief]

Hi,

lets assume there is no g (g=inf).

notice the the sum end at the index n, not N.

I'm trying to see directly the convolution theorem but I get stuck:
View attachment 2233

The problem is that the second sum depends on k so the double sum doesn't factor to the product of DFTs.

what am I missing?

thank you