Diagonalizing a Matrix: Understanding the Process and Power of Matrices

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this,

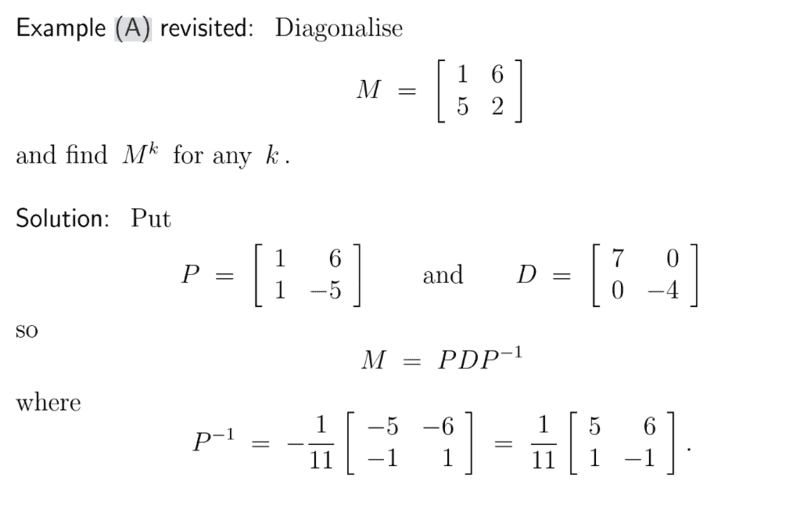
Dose someone please know where they get P and D from?

Also for $M^k$, why did they only raise the the 2nd matrix to the power of k?

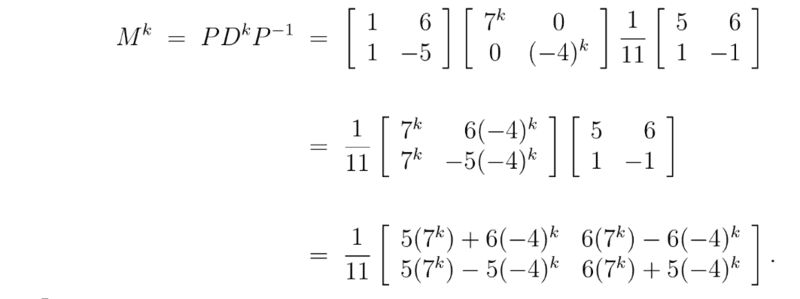
Many thanks!

 

[fresh_42]

You calculate the eigenvalues of $M$ and this gives you $D$. I would solve the resulting linear equation system $PM=DP$ and treat $P$ as variables. The correct way is the Gauss-Jordan algorithm
https://en.wikipedia.org/wiki/Gaussian_elimination
( or https://de.wikipedia.org/wiki/Gauß-Jordan-Algorithmus with Chrome and Translate )

The eigenvalues are the zeros of $\det(M-xI)=(1-x)\cdot (2-x) -5\cdot 6=0.$

 

[martinbn]

Also for $M^k$, why did they only raise the the 2nd matrix to the power of k?

Just add, that they are raising the whole thing to power $k$, but you didn't notice that many things cancel.
$M^k=(PDP^{-1})^k=PDP^{-1}PDP^{-1}\dots PDP^{-1}=PDD\dots DP^{-1}=PD^kP^{-1}$

 

[Mark44]

Dose someone please know

I'm trying to train you to know the difference between "dose" and "does" but have been unsuccessful so far.

 

[SammyS]

I'm trying to train you to know the difference between "dose" and "does" but have been unsuccessful so far.

Is there no antidote (or perhaps - antidose) for this?