Did I Calculate Velocity and Acceleration Correctly?

[Lancelot59]

This problem kicked me and I ended up using all my attempts. I just realized I probably failed this part because I used radian input while my calculator was set to degree mode.

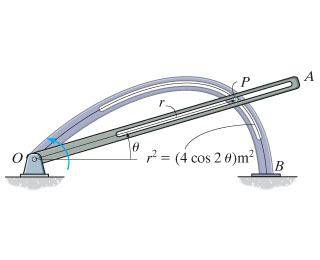
OA rotated counterclockwise:
$$\theta'=3t^{\frac{3}{2}} rad/s$$
When t=0 theta=0. Find the magnitude of velocity and acceleration when theta=30 degrees.

I went about finding some stuff first:
$$\theta=\frac{6}{5}t^{\frac{5}{2}} rad/s$$
$$\omega=\theta'=3t^{\frac{3}{2}} rad/s$$
$$\alpha=\theta''=\frac{9}{2}t^{\frac{1}{2}} rad/s$$
And I isolated the applicable part of the curve:
$$r=+\sqrt{4cos(2\theta)$$

I also solved for time at 30 degrees and got 0.717674 seconds.

I didn't fall into the trap of just using the angular velocity as the answer. I actually only could find the tangential velocity via this equation:
$$v_{tangental}=\omega*r$$
$$v_{tangental}=3t^{\frac{3}{2}}*\sqrt{4cos(2\theta)$$
$$v_{tangental}=3(0.717674)^{\frac{3}{2}}*\sqrt{4cos(2(\frac{\pi}{6}))$$
$$v_{tangental}=2.87944975 m/s$$
Which I got using the correct calculator mode this time.

PROBLEM:
How can I go about getting centripetal velocity?

As for acceleration I used this setup:
$$a_{tangental}=\alpha*r$$
$$a_{tangental}=\sqrt{4cos(2\theta)*\frac{9}{2}*t^{\frac{1}{2}}$$

$$a_{centripetal}=\frac{v_{tangental}}{r}$$
$$a_{centripetal}=\frac{v_{tangental}}{\sqrt{4cos(2 \theta)}}$$
Substituted in tangental velocity, took the magnitude and got a wrong answer, hopefully only because I had the wrong mode on my calculator.

Did I do this right or am I just silly?

 

[NateD]

The process you used to calculate the tangential velocity and acceleration is correct. However, when calculating the magnitude of the centripetal velocity, you should have used the equation:v_{centripetal} = \omega * r where \omega is the angular velocity. This is because the centripetal velocity is simply the product of the angular velocity and the radius (or in this case, the length of the arc). With that said, once you have calculated the centripetal velocity, you can calculate the centripetal acceleration by using the equation: a_{centripetal} = \frac{v_{centripetal}^2}{r}Hope this helps!