Diff eq, Spring/mass damped/driven-Am I doing this right?

[frozenguy]

Diff eq, Spring/mass damped/driven--Am I doing this right?!

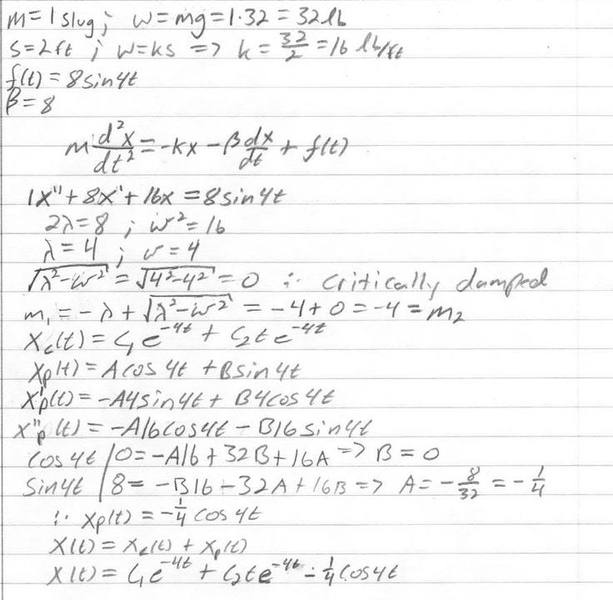
Homework Statement

1.) After a 10lb weight is attached to a 5ft spring, the spring measures 7ft. The 10lb is replaced with 8lb, and placed in a medium offering resistence equal to the instantaneous velocity.
A) find the equation of motion if the weight is released 0.5ft below equilibrium with downward vel of 1ft/s.

B) What are the amplitude and period of the motion? How many complete vibrations does the weight complete in $$2\pi$$ seconds?

C) Find the times at which the weight passes through the equilibrium position heading downward.


2.) A mass of 1 slug, when attached to a spring, stretches it 2ft and then comes to rest in the equilibrium position. Starting at t=0, an external force equal to f(t)=8sin4t is applied to the system. Find the equation of motion if the surrounding medium offers a damping force numerically equal to 8 times the instantaneous velocity.

Thanks..

The Attempt at a Solution

1.)

2.) I left it with C₁ and C₂ b/c no initial cond were given.

 

[lippyka]

A) mx" + kx + cv = F(t) mx" + 8v + 8x = 8sin4t B) Amplitude: ? Period: 2\pi/4 Complete vibrations: \pi/2 C) t1=0, t2=2\pi/4