Difference between a closed solid and a Cartesian surface

[Amaelle]

Homework Statement

look at the image

Relevant Equations

-closed solid
-cartesian surface
-Divergence theorem

Greetings All!

I have hard time to make the difference between the equation of a closed solid and a cartesian surface.

For example in the exercice n of the exam I thought that the equation was describing a closed solid " a paraboloid locked by an inclined plane (so I thought I could use the divergence theorem) while it was describing a broken paraboloid (a cartesian surface). I joined the exercice to be more precise.

I hope I could explain my problem.

Thank you

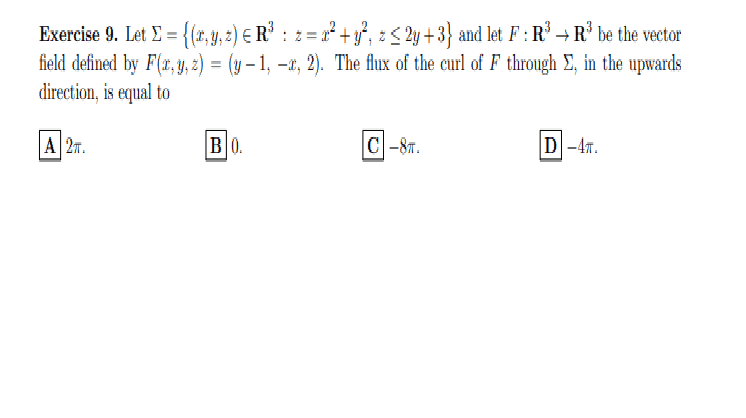
Best regards.

 

[Orodruin]

You are told that $z= x^2 + y^2$ on $\Sigma$. This is not generally true on the plane that would close the surface.

 

[FactChecker]

Any time a set in $R^n$ has an equal sign, "=", in the definition, there is no n-dimensional volume to the set, so it is a surface (boundary?). So $z = x^2 + y^2$ implies that it is a surface.

 

[Amaelle]

Any time a set in $R^n$ has an equal sign, "=", in the definition, there is no n-dimensional volume to the set, so it is a surface (boundary?). So $z = x^2 + y^2$ implies that it is a surface.

thank you very much Z= something means surface !

 

[Amaelle]

You are told that $z= x^2 + y^2$ on $\Sigma$. This is not generally true on the plane that would close the surface.

the plane that would close the surface would have been z=2y+3

 

[Orodruin]

the plane that would close the surface would have been z=2y+3

Note: If you had been told z=2y+3 instead of $z\leq 2y+3$, your set would have been a one-dimensional curve (the intersection of the two surfaces). Here you are told that you have a single surface (the parabola) and that it is the part of the parabola inside a given volume (given by the inequality).

 

[Amaelle]

Note: If you had been told z=2y+3 instead of $z\leq 2y+3$, your set would have been a one-dimensional curve (the intersection of the two surfaces). Here you are told that you have a single surface (the parabola) and that it is the part of the parabola inside a given volume (given by the inequality).

yes thanks a million!