Different norms and how L1 leads to the sparsest solution

[fog37]

TL;DR Summary

Understand why L0 and L1 lead to the sparsest solution of a linear system of equations

Hello,

I think I understand the different types of norms that we can calculate for a vector living in a finite dimensional space. Each norm has its own benefits.

In 2D, for simplicity, all vectors with the same $L2$ norm are points on a circle (the isoline). All vectors with the same $L1$ are points on the diamond with vertices on the axes. and all vectors with the same $L0$ are points on

Question: what is the concept of regularization penalty that I have read about in regards to norms?

Question: in solving an underdetermined system of linear equations (more unknown that equations), why does looking looking for the $l-1$ norm promotes finding the sparsest solution?
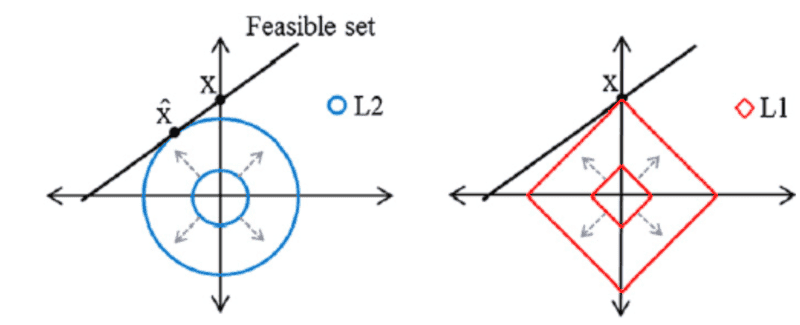
For example, in the figure below, the black straight line represents all possible and infinite solutions of the underdetermined system. We need to find a solution (which is where it the ball touches the black line) which is required to be sparse...The $L1$ solution is the sparsest since it has only one nonzero coordinate... But doesn't it all depend on the position of the black line of solutions? For example, the solution black line could be positioned in such a way that it perfectly overlaps one of the sides of the diamond. Or the black line could touch the circle (L2) where the solution is sparse if the black line was vertical or horizontal...I am confused...

The best norm, when looking for the sparsest solution of a system, is the L0 norm but it does not actually satisfy the property of being convex...

 

[Office_Shredder]

For the $L_0$ norm the penalty function is literally the number of nonzero elements, so it has to give the sparsest solution possible.

The $L_2$ norm has the property that the partial derivative with respect to any coordinate at 0 is 0, so if you have some coordinate that is non zero and some coordinate that is zero, you generally can modify the 0 coordinate by a lot, in exchange for making the nonzero coordinate only a little smaller, and still reduce the penalty function. The $L_2$ norm basically guarantees that every coordinate is nonzero, because there's no penalty for making that happen just a little bit.

The only time you get a zero coordinate is when changing it doesn't let you modify the other coordinates at all, which corresponds to when the solution set happens to be a vertical or horizontal line in your diagram.

The $L_1$ norm sits in the middle. If you have a coordinate whose value is 0, you have to increase it by less than the amount you can decrease all the other coordinates in order to make your penalty function smaller. For example if you consider solutions to $x-2y=1$, for every unit that I change $x$ by, I only have to change $y$ by 0.5 units. So if I have a random solution, say $x=19$ and $y=9$, I know if I move $x$ to make it smaller, then even if that ends up making $y$ larger, the $L_1$ norm is guaranteed to decrease. This means I might as well make $x$ zero.

In general the only time you don't get to win to this is when you have something like $x+y=1$ which corresponds to the solution set being parallel to the face of the unit ball like you observed.

Notice that even when the $L_2$ norm finds a solution with one zero in it, the $L_1$ norm finds it also. And when the $L_1$ norm doesn't guarantee finding a sparse solution, the $L_2$ norm yields the least sparse solution possible (both coordinates being equal), and the sparse solution of one zero coordinate is at least one of the possible $L_1$ minimizing solutions.