Thorra
- 45
- 0
So in this thread I plan to present 3 problems and my takes on them. I think I'll post each next one after I get some help and solution with the current one.
Note that this is a translated problem from my native language.
Task Nr. 1
Write the difference analogue (I mean in discrete form) to a parabolic type operator $$Lv(x,y,t)=\frac{\partial v}{\partial t} - \left(\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2}\right) $$, if the time step is $\tau$, and the steps by space coordiates are respectively $g$ and $h$.
Using the Taylor series, find out the difference operator's local order of approximation.
Graphically show the respective difference operator pattern with respective coefficients.
Graphically show the equation's $Lv(x,t)=0$ (with one space coordinate) the respective linear algebraic equation system's structure matrix and in vector form in the new time moment (layer) $t^{j+1}$, if the issued differential equation gets additional conditions: $v(a,t)=c_1 (t)_0 ; v(b,t)=c_2 (t)_1 v(x,0)=c_3 (x)$My take
So I took t as the z coordinate. Wrote this:
$$L^{(0)}_{g,h,\tau} v - L_\tau v -L_g v - L_h v = \frac{v_{i,j}^{k+1} - 2v_{i,j}^k}{\tau} - \frac{v^k_{i+1,j} - v_{i,j}^k + v_{i-1,j}^k}{g^2} - \frac{v^k_{i,j+1} - 2v_{i,j}^k + v_{i,j}-1^k}{h^2}$$
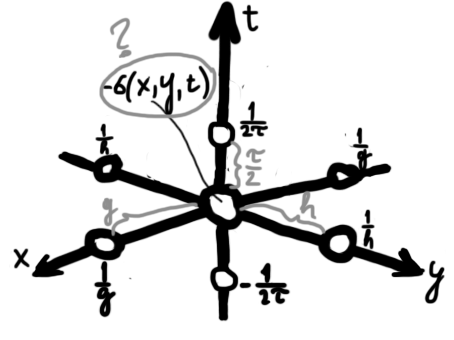
I didn't figure out how to find out the local order of approximation and much less the last requirement, but I figured the pattern image must look something like this (sorry for the poor quality, will draw better next time):
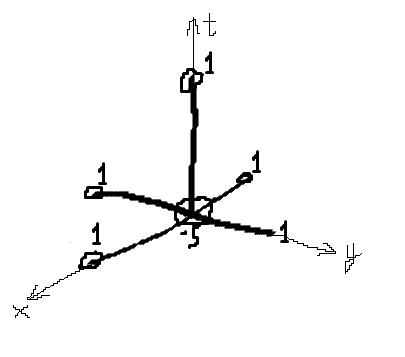
Though I don't know about the coefficients, it's just something a coursemate suggested to another coursemate on a similar problem.
Any thoughts on how to legitimately find out the local approximation and that later more advanced thing? And if even what I got is correct in any way? I got 0 points for this.
Thank you for your attention.
Note that this is a translated problem from my native language.
Task Nr. 1
Write the difference analogue (I mean in discrete form) to a parabolic type operator $$Lv(x,y,t)=\frac{\partial v}{\partial t} - \left(\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2}\right) $$, if the time step is $\tau$, and the steps by space coordiates are respectively $g$ and $h$.
Using the Taylor series, find out the difference operator's local order of approximation.
Graphically show the respective difference operator pattern with respective coefficients.
Graphically show the equation's $Lv(x,t)=0$ (with one space coordinate) the respective linear algebraic equation system's structure matrix and in vector form in the new time moment (layer) $t^{j+1}$, if the issued differential equation gets additional conditions: $v(a,t)=c_1 (t)_0 ; v(b,t)=c_2 (t)_1 v(x,0)=c_3 (x)$My take
So I took t as the z coordinate. Wrote this:
$$L^{(0)}_{g,h,\tau} v - L_\tau v -L_g v - L_h v = \frac{v_{i,j}^{k+1} - 2v_{i,j}^k}{\tau} - \frac{v^k_{i+1,j} - v_{i,j}^k + v_{i-1,j}^k}{g^2} - \frac{v^k_{i,j+1} - 2v_{i,j}^k + v_{i,j}-1^k}{h^2}$$
I didn't figure out how to find out the local order of approximation and much less the last requirement, but I figured the pattern image must look something like this (sorry for the poor quality, will draw better next time):

Though I don't know about the coefficients, it's just something a coursemate suggested to another coursemate on a similar problem.
Any thoughts on how to legitimately find out the local approximation and that later more advanced thing? And if even what I got is correct in any way? I got 0 points for this.
Thank you for your attention.