- #1
sorter
- 47
- 0
Has to convert B6-1 into B6-2 Source Transport Phenomenon 2nd ed -
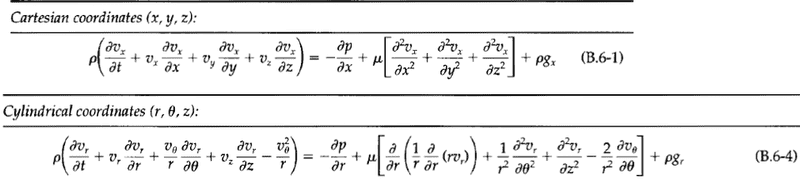
Differential Cartesian Coordinates Into Cylindrical Coordinates
- Thread starter sorter
- Start date
Click For Summary
Homework Help Overview
The discussion revolves around converting differential Cartesian coordinates into cylindrical coordinates, specifically in the context of transport phenomena as outlined in a textbook.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning
Approaches and Questions Raised
- Participants are attempting to understand how to convert velocity components from Cartesian to cylindrical coordinates, particularly focusing on the relationships between the components and questioning how to derive the angular component.
Discussion Status
Some participants are actively engaging with the problem, seeking to clarify the relationships between the different coordinate systems. Guidance has been offered to set up relevant quantities and relationships, indicating a collaborative effort to explore the topic further.
Contextual Notes
There appears to be some uncertainty regarding the conversion of specific velocity components, particularly the transition from Cartesian subscripts to cylindrical coordinates. Participants are navigating through the definitions and relationships involved in this conversion.
Similar threads
- · Replies 21 ·
- · Replies 4 ·
- · Replies 6 ·
- · Replies 6 ·
- · Replies 6 ·
- · Replies 17 ·
- · Replies 4 ·
- · Replies 24 ·