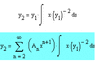Differential Equation: Frobenius

[jason17349]

My problem: find the first solution and use it to find the second solution for

x^2*y"-x*y'+(x^2+1)y=0

assuming y=summation from n=0 to infinity for An*x^n+r

substituting and solving gives me r=1 and a general equation: An=A(n-2)/((n+r)*(n+r-2)+1) for n >= 2

plugging r into my general equation gives An=A(n-2)/((n+1)*(n-1)+1) for n >= 2

plugging n into this I get y=A0*x+(1/4)A0*x^3+(1/64)A0*x^5+(1/2304)A0*x^7... this is y1

now y2=y1*v

I'm not entirely sure what to do after this because I'm unable to reduce y1 to a simple summation which is the only way I've seen this problem done before. Or am I going about this the wrong way?

 

[jason17349]

Using the reduction formula I came up with this solution:

y2=y1*integral(x*(y1)^(-2)*dx)

I don't know how to write math symbols in here so I attached a picture that is easier to understand.

does this seem like the correct solution? I'm also concerned about my answer for y1. The index value and power particularly.

 

[dextercioby]

We have a LaTex enabled forum.Just type the code and the compiler will do it all.More u can read here:https://www.physicsforums.com/showthread.php?t=8997

Daniel.

 

[rick1138]

Get a copy of Schaum's Outline of Differential Equations - it has an excellent chapter on Frobenius methods.

 

[saltydog]

You know, I think I'm makin' progress with this one. For starters, I get a different recurrence relation. First though, the indicial equation is:

$$c^2-2c+1$$

The double roots (1,1), indicate a logarithm solution. However, when I do the arithemetic, I get (for the first solution):

$$a_n=-\frac{a_{n-2}}{(n+c)(n+c-2)+1}\quad\text{for}\quad n\geq 2$$


Now, [itex]a_0[/tex] should not be zero but $a_1$ can. Thus, I get for the first solution:

$$y_1(x)=x^c+\sum_{n=2}^{\infty} a_n(c)x^{n+c} \quad\text{with}\quad a_0=1 \quad\text{and}\quad a_1=0$$

The second one, well, we'll take some partials, express it in terms of a harmonic series, you know, what that have in the book. Anyway, that's where I'm goin' with it. I tell you what though, when I check the first solution against both numerical estimates and back substitution, the results seems to indicate it is correct (as a particular solution that is), we'll add some constants later.

Really, I'd like it in the differential equation section but . . . nevermind.

 

[saltydog]

Jason, you still with me? Or have you finished the semester and never want to see another differential equation ever again? Anyway, I got both solutions via the logarithm method and if you guys don't mind, I'd like to complete this problem. I've simplified the first solution:

$$y_1(x)=x+\sum_{n=1}^{\infty} \frac{(-1)^n}{2^{2n}(n!)^2}x^{2n+1}$$

I've attached a plot. Keep in mind it's a "particular solution". Once we have both solutions, we'll add some arbitrary constants to make up the general solution.

The second one is more interesting . . .

 

[saltydog]

In order to find the second solution, leave $a_n$ in its general form:

$$a_n(c)=\frac{(-1)^n}{[c(2+c)+1][(4+c)(2+c)+1][(6+c)(4+c)+1]...[(2n+c)(2n+c-2)+1]}$$

The first solution is then:

$$y_1(x)=x^1+\sum_{n=2}^{\infty}a_n(1)x^{2n+1}$$

And the second:

$$y_2(x)=[\frac{\partial y(x,c)}{\partial c}]_{c=1}$$

$$=y(x,1)ln(x)+\sum_{n=1}^{\infty}a_n^{'}(1)x^{2n+1}$$

The difficult part is finding the derivative of $a_n(c)$ with respect to c.

This is accomplished by logarithmic differentiation. Anyway, it turns out that:

$$a_n^{'}(1)=\frac{(-1)^{n+1}}{2^{2n}(n!)^2}\sum_{k=1}^{n}\frac{1}{k}$$

With:

$$H(n)=\sum_{k=1}^{n}\frac{1}{k}$$

Then:

$$y_2(x)=y_1(x)ln(x)+\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{2^{2n}(n!)^2}H(n)x^{2n+1}$$


Thus finally we have the general solution:

$$y(x)=Ay_1(x)+By_2(x) \quad\text{with}\quad x>0$$

With A and B arbitrary constants.

So, what do I do if I have an initial problem with this mess? You know, the differential equation with:

$$y(a)=h \quad\text{and}\quad y^{'}(a)=k$$

Well, calculate the derivative of y(x). That's doable. Then we're left with:

$$h=Av+Br$$

$$k=As+Bp$$

And then solve for A and B. I did that for:

$$y(0.1)=2.4$$

$$y^{'}(0.1)=-1.6$$

This yields:

$$y(x)=-34.3991y_1(x)-25.4162y_2(x)$$

The first plot is this particular solution.
The second plot is a numerical analysis of the differential equation with these conditions.
The third plot is a superposition of both.

Edit: I used the first 125 terms of the series.

 

[jason17349]

Haha, yeah I have finished the semester and while I never want to see one of these again this question is nagging me. I just came back from class so I'll go ahead and show you what I turned in.

After going back and cleaning my notation up I got the same initial answer for y:

$$y_1=a_0x+\sum_{n=2}^{\infty} a_nx^{n+1}$$

From here I used a method I have copied down in my notes, I believe it was related to the reduction method. Don't know if this was correct or not but it's too late now.

Using this method I began with

$$y_2=y_1v$$ all of which are functions of x I just don't feel like writing it over and over

which leads to

$$y'_2=y_1v'+y'_1v$$

$$y''_2=y_1v''+2y'_1v'+y''_1v$$

These were subbed back into the original formula replacing the y's giving:

$$v''x^2y_1+2v'x^2y'_1+vx^2y''_1-v'xy_1+vxy'_1+v(x^2+1)y_1=0$$

Then combining like terms of v:

$$v(x^2y''_1+xy'_1+(x^2+1)y_1)+v''x^2y_1+v'(2x^2y'_1-xy_1)=0$$

the term $$v(x^2y''_1+xy'_1+(x^2+1)y_1)$$ then goes away for reasons I don't fully understand. leaving:

$$v''x^2y_1+v'(2x^2y'_1-xy_1)=0$$

now set

$$u=v'$$
$$u'=v''$$

and substituting

$$u'x^2y_1+u(2x^2y'_1-xy_1)=0$$

rearranging gives:

$$\frac{u'}{u}=-2\frac{y'_1}{y_1}+\frac{1}{x}$$

Recalling that these are all functions of x I can integrate them easily

$$\ln(u)=-2\ln(y_1)+\ln(x)$$

$$u=y_1^{-2}x$$

$$v'=y_1^{-2}x$$

$$v=\int{y_1^{-2}xdx}$$

$$y_2=y_1v$$

$$y_2=y_1\int{y_1^{-2}x}dx$$

$$y_2(x)=(a_0x+\sum_{n=2}^{\infty} a_nx^{n+1})\int{(y_1(x))^{-2}x}dx$$

So there it is. A bit long winded but I wanted you to see my whole though process. Is it garbage? Let me know.

 

[saltydog]

the term $$v(x^2y''_1+xy'_1+(x^2+1)y_1)$$ then goes away for reasons I don't fully understand. leaving:

Very nice Jason. The term goes away simply because $y_1(x)$ is a solution to the homogeneous equation. That is, when you operate on it with that Differential operator, you get zero. Thanks for taking the time to show me that method. As far as the solution, don't know if your teacher will be picky and ask what is $a_1$? Note in my solution, I set it to zero which means all even powers of x drop out. But it's summer time now anyway. Enjoy the break.

 

[jason17349]

Yeah, I also set $$a_1$$ to 0 I noted this on the work I turned in. Thank you for helping me.

 

[dextercioby]

You know,Salty,that H(x) that u used,it's actually linked to the $\psi$ function.You may want to check it out.

Daniel.

 

[saltydog]

These were subbed back into the original formula replacing the y's giving:

$$v''x^2y_1+2v'x^2y'_1+vx^2y''_1-v'xy_1+vxy'_1+v(x^2+1)y_1=0$$

Then combining like terms of v:

$$v(x^2y''_1+xy'_1+(x^2+1)y_1)+v''x^2y_1+v'(2x^2y'_1-xy_1)=0$$

the term $$v(x^2y''_1+xy'_1+(x^2+1)y_1)$$ then goes away for reasons I don't fully understand. leaving:

I wish to correct something for both Jason and I: When substitutiting back into the ODE, the first term should be:

$$v(x^2y''_1-xy'_1+(x^2+1)y_1)$$

And that's why it's zero since the term in parenthesis is 0 (a homogeneous ODE, i.e., the original equation). I tell you what though, the expression:

$$\int(y_1(x))^{-2}xdx$$

is a problem but Volterra left solutions in much worst shape and his rational was to get the problem to a "solution expression".

 

[starfinder]

The difficult part is finding the derivative of $a_n(c)$ with respect to c.
This is accomplished by logarithmic differentiation. Anyway, it turns out that:
$$a_n^{'}(1)=\frac{(-1)^{n+1}}{2^{2n}(n!)^2}\sum_{k=1}^{n}\frac{1}{k}$$

With:
$$H(n)=\sum_{k=1}^{n}\frac{1}{k}$$

Could someone, please, explain in details how this part is done? I understand how logarithmic differentiation works but I never do it right when searching for the second solution in cases like this. I guess the factorials trouble me. Any help?