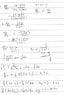Differential equation of dy/dx = (2x-y+4)/ (4x-2y +1)

[hotjohn]

Homework Statement

I'm asked to use the transformation of v= 2x-y to solve dy/dx = (2x-y+4)/ (4x-2y +1) the answer given is (2/9)(6x-3y-2) +(7/9)ln(6x-3y-2) = x +c , i got (2/9)(6x-3y) +(7/9)ln(6x-3y-2) = x +c , what's wrong with my working ?

Homework Equations

The Attempt at a Solution

 

[mfb]

The two answers differ by a constant summand of 4/9. As you have "+c" anyway, this difference does not matter.

 

[hotjohn]

The two answers differ by a constant summand of 4/9. As you have "+c" anyway, this difference does not matter.

lol , why the author want to dd in another (2/9)(-2) into the answer ? this is confusing ...

 

[HallsofIvy]

Presumably, because the author used a different method to arrive at a solution. In any case, the point is that, because the derivative of a constant is 0, two functions, differing by a constant, can be solutions to the same first order differential equation.