- #1
lclauber
- 2
- 0
Differential Equation Power Series Method (Almost done!)
solve (2x-1)y'+2y=0 using power series.
I'm really close to the correct answer, which is c/(1-2x). I keep getting 2c/(1-2x).
I got the correct radius of convergence, however (1/2)
shown in my attempt at a solution.
attached as a png.
Homework Statement
solve (2x-1)y'+2y=0 using power series.
I'm really close to the correct answer, which is c/(1-2x). I keep getting 2c/(1-2x).
I got the correct radius of convergence, however (1/2)
Homework Equations
shown in my attempt at a solution.
The Attempt at a Solution
attached as a png.
Attachments
Last edited:
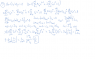
 …
…