Graham87
- 72
- 16
- TL;DR Summary
- Differential equation using power series method
I am attempting to solve this differential equation with power series
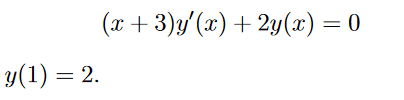
I came with the following solution but I doubt it is correct.
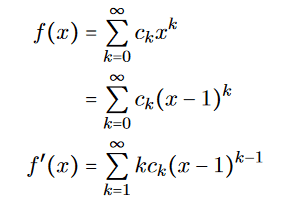
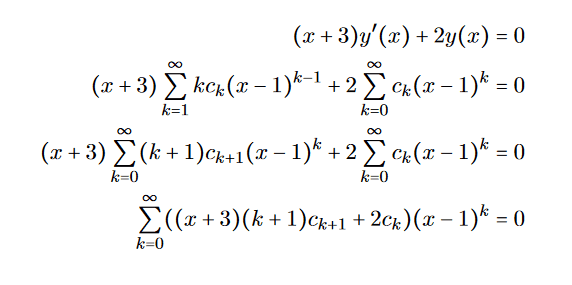
Since x=1 we get:
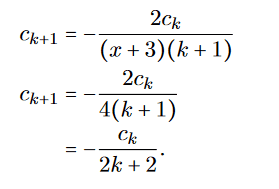
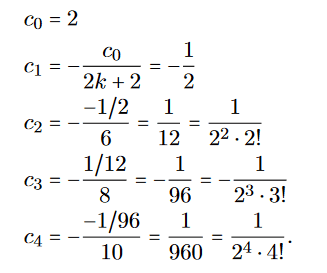
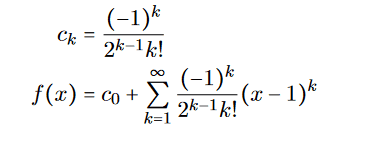
I doubt its correctness because it looks messy. Also the convergence radian R goes to 0, giving only a solution for x=0 which is not correct, since the beginning condition states y(1)=2.
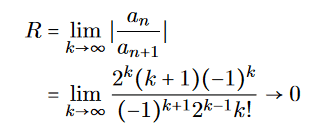
I came with the following solution but I doubt it is correct.
Since x=1 we get:
I doubt its correctness because it looks messy. Also the convergence radian R goes to 0, giving only a solution for x=0 which is not correct, since the beginning condition states y(1)=2.
Attachments
Last edited:
