- #1
whoopie88
- 52
- 0
Difficult Ladder Against Wall Torque Problem!
An 85 kg person stands on a uniform 6.6 kg ladder that is 3.9 m long, as shown. The floor is rough; hence it exerts both a normal force, f1, and a frictional force, f2, on the ladder. The wall, on the other hand, is frictionless; it exerts only a normal force, f3. Using the dimensions in the figure, find the magnitudes of f1, f2, and f3.
All forces and torque formulas.
I found f1 - 898.6 N. I can't find f2 and f3, which I think are supposed to be equal. No matter what I try, I can't seem to get an answer. Here's my work:
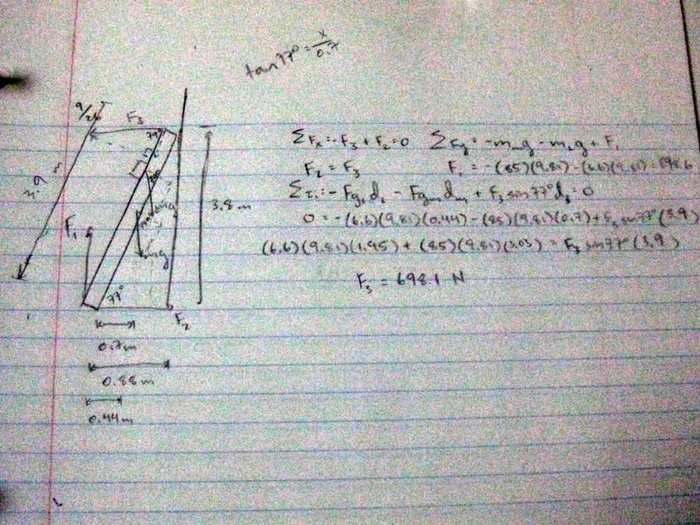
Help please? Thanks in advance.
Homework Statement
An 85 kg person stands on a uniform 6.6 kg ladder that is 3.9 m long, as shown. The floor is rough; hence it exerts both a normal force, f1, and a frictional force, f2, on the ladder. The wall, on the other hand, is frictionless; it exerts only a normal force, f3. Using the dimensions in the figure, find the magnitudes of f1, f2, and f3.
Homework Equations
All forces and torque formulas.
The Attempt at a Solution
I found f1 - 898.6 N. I can't find f2 and f3, which I think are supposed to be equal. No matter what I try, I can't seem to get an answer. Here's my work:
Help please? Thanks in advance.