Difficult Understanding Magnitude and Phase Shift of Transfer Function

[wellmoisturizedfrog]

TL;DR Summary

I am unsure if my current understanding of transfer functions is correct.

Hello,

My textbook offers the following transfer function as an example.

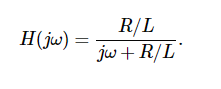
It then goes on to explain that the following equations represent the magnitude and phase shift of the transfer function.

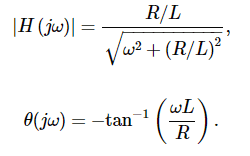
However, I am having some difficulty jumping from the first equation to these equations. From my understanding, in order to find the magnitude of the transfer function, the magnitude of the complex number in the denominator is found. I'm not sure if this logic is correct.

I am also unsure about how the equation for the phase shift of the transfer equation has a negative sign in front. I understand the other aspects of it, though.

I would appreciate any clarifications.

 

[scottdave]

Plotting the complex numbers graphically may help you understand why the denomiator is that way.

Multiply numerator and denominator by complex conjugate of denominator should help understand the angle.

 

[hutchphd]

Multiply numerator and denominator by complex conjugate of denominator should help understand the angle.

And the magnitude as well......this is the standard way to manipulate complex numbers.

 

[DaveE]

https://www.khanacademy.org/math/pr...df:complex-abs-angle/v/basic-complex-analysis

 

[wellmoisturizedfrog]

Ah I see, thank you for the insight! I appreciate the insight and resources.