- #1
Estudiante Curioso
- 2
- 1
1. Problem
A boatman crosses a river of width ##D## from a point ##O##, looking to get to point ##A## on the opposite riverbank. Suppose that the flowrate is uniform with velocity of magnitude ##v_0##. The boat has a velocity ##\vec{v_1}## relative to the water, with constant magnitude, and it always points towards the point ##A##. Calculate the time that the boatman takes to ge t to point ##A##.
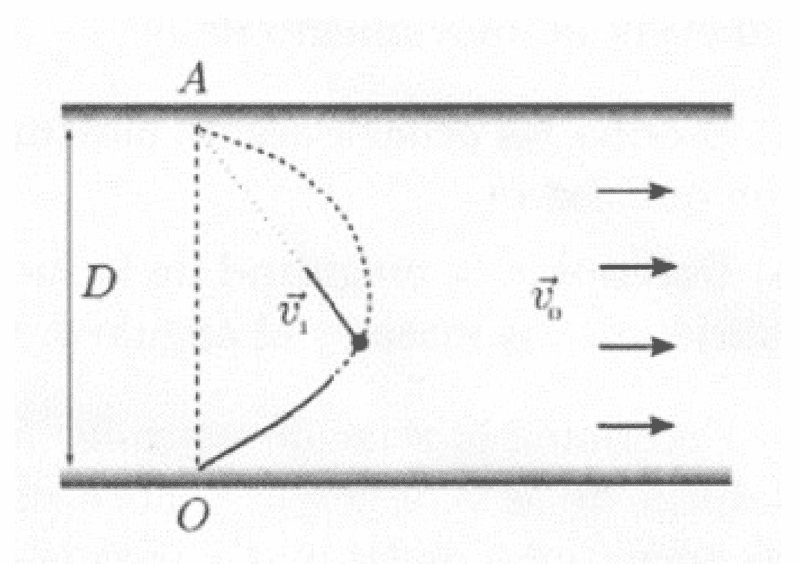
We were also hinted that it may be useful to state that ##\vec{r_A}-\vec{r_B}=\alpha(t)\vec{v_1}## (because ##\vec{v_1}## points to ##A##), and then derive that expression.
2.The attempt at a solution
First I noticed that since ##||\vec{v_1}||## is constant, its derivative must be perpendicular to it. So the plan was to project ##\vec{v_b}## (obtained from the previous derivative) over the unitary vectors ##\hat{\vec{v_1}}## and ##\hat{\dot{\vec{v_1}}}## and then I would get two expressions from the previous derivative, from where I could potentially obtain ##\alpha(t)## through integration or a differential equation. I also noted that those unitary vectors define polar coordinates with respect to ##A##.
I arrived to the expressions $$v_1+\vec{v_0} \hat{v_1} = \alpha'(t) v_1$$ and $$v_0 \hat{\dot{\vec{v_1}}}= \alpha(t) ||\dot{\vec{v_1}}||$$
where I could use trigonometry to replace the dot products on the left with ##sin(\theta)## and ##cos(\theta)## (where ##\theta## is the angle between ##\vec{v_0}## and ##\vec{v_1}##), but I am completely puzzled as what to do with ##||\dot{\vec{v_1}}||## and if this method actually works.
A boatman crosses a river of width ##D## from a point ##O##, looking to get to point ##A## on the opposite riverbank. Suppose that the flowrate is uniform with velocity of magnitude ##v_0##. The boat has a velocity ##\vec{v_1}## relative to the water, with constant magnitude, and it always points towards the point ##A##. Calculate the time that the boatman takes to ge t to point ##A##.
We were also hinted that it may be useful to state that ##\vec{r_A}-\vec{r_B}=\alpha(t)\vec{v_1}## (because ##\vec{v_1}## points to ##A##), and then derive that expression.
2.The attempt at a solution
First I noticed that since ##||\vec{v_1}||## is constant, its derivative must be perpendicular to it. So the plan was to project ##\vec{v_b}## (obtained from the previous derivative) over the unitary vectors ##\hat{\vec{v_1}}## and ##\hat{\dot{\vec{v_1}}}## and then I would get two expressions from the previous derivative, from where I could potentially obtain ##\alpha(t)## through integration or a differential equation. I also noted that those unitary vectors define polar coordinates with respect to ##A##.
I arrived to the expressions $$v_1+\vec{v_0} \hat{v_1} = \alpha'(t) v_1$$ and $$v_0 \hat{\dot{\vec{v_1}}}= \alpha(t) ||\dot{\vec{v_1}}||$$
where I could use trigonometry to replace the dot products on the left with ##sin(\theta)## and ##cos(\theta)## (where ##\theta## is the angle between ##\vec{v_0}## and ##\vec{v_1}##), but I am completely puzzled as what to do with ##||\dot{\vec{v_1}}||## and if this method actually works.
Attachments
Last edited: