Diffraction from a set of concentric rings with random phase

[Gezstarski]

TL;DR Summary

Looking for a treatment of the focussing properties of a set of concentric rings with random phase

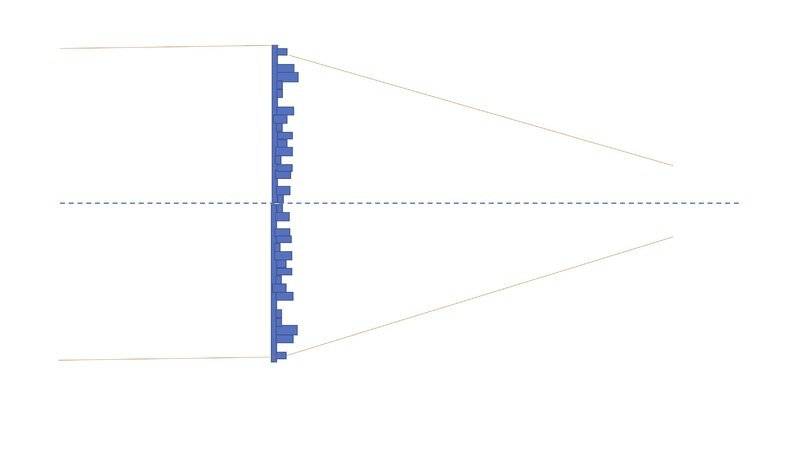
I have been considering the properties of a Diffractive Optical Element (DOE) consisting of a very large number of concentric rings of equal (small) width, where the thicknessses of the rings are such as to produce random phase shifts in the range 0 to 2pi. I think I understand the behaviour of such a DOE - it acts as a diffraction limited lens that is achromatic but of exceedingly low efficiency. I am sure that this problem must have been tackled before but I have not been able to find a reference or a textbook treatment. Can anyone help?

 

[tech99]

Each ring emits radiation of random phase. So there is no preferred direction of radiation. It is behaving like a white surface. It looks as if the incoming energy is re-radiated isotropically.

 

[Gezstarski]

Its not as simple as that. Each ring individually would produce a diffraction pattern with a wave amplitude that is a J_0 Bessel function, with a peak on the axis and lower elsewhere. At any point in the image plane the J_0 contributions from all the rings combine with random phases, but just as the steps of a random walk will almost always add up to a net displacement, the expectation value for the intensity is non-zero. And on-axis, where all the contributions are largest, the resultant intensity will be highest - a random walk of N large steps ends up further away than one with N small steps.

For a random walk with steps of equal length L the mean square displacement after N steps is N L but the present case is a not quite the classical random walk one because at a given point in the image plane the contributions from the different rings are not equal. Its a random walk with a distribution of step lengths.

The net effect is a PSF (point source response function) that has a core rather like an Airy pattern in shape but very much reduced in amplitude and with stronger side lobes. In the figure the PSF has been normalised by a factor 3N/4. Most of the flux does indeed get scattered to wide angles but there is a central spot far brighter than the background.