- #1
Bolter
- 262
- 31
- Homework Statement
- See image below
- Relevant Equations
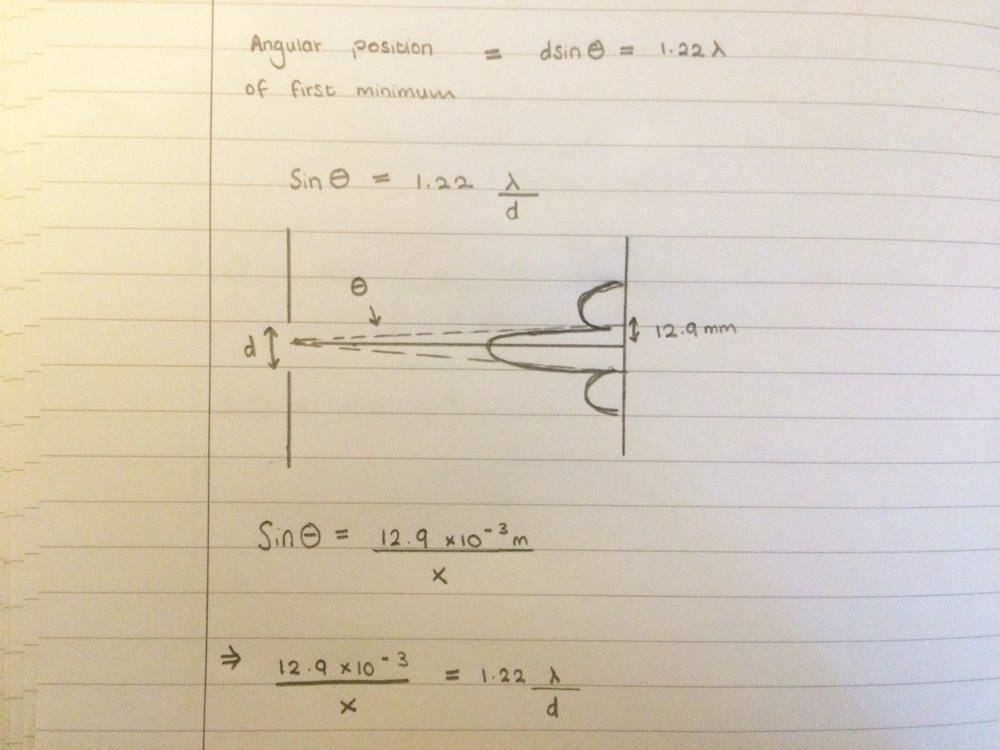
- dsin(theta) = 1.22 lambda
Here is the following question I have been trying to answer

I have drawn a quick simple sketch of what I believe is happening in the set up.
Also because the angle that I am dealing with is very small, I made the assumption that sin(theta) = 12.9mm/X (where X in this case is the max distance I need from the observer)
Any help would be much appreciated! Thanks
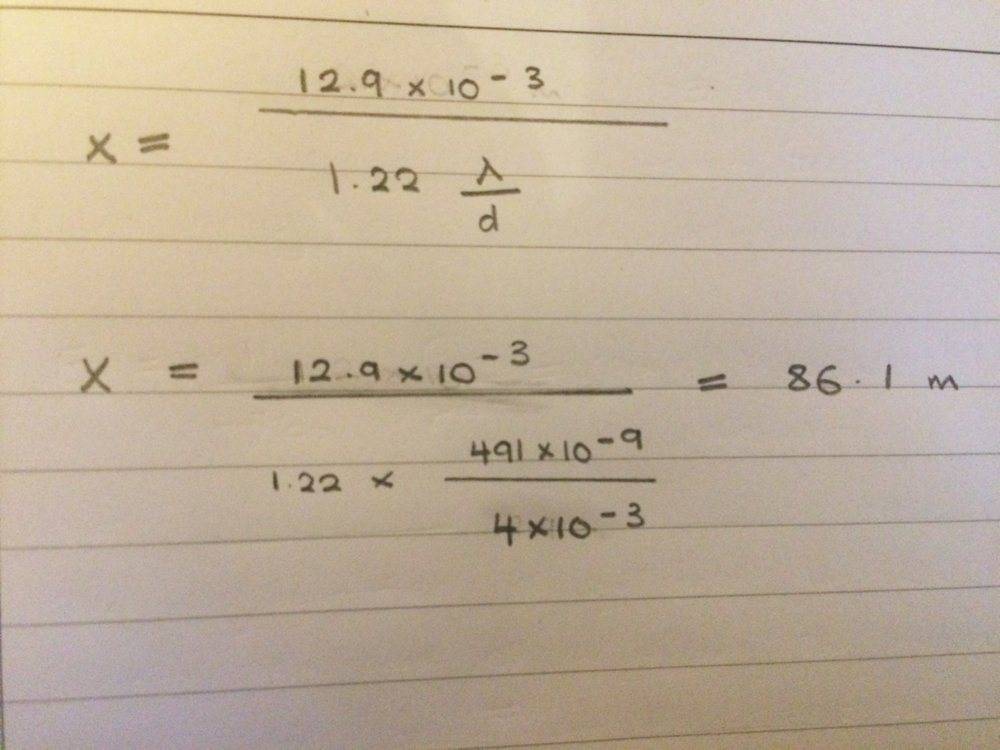
I have drawn a quick simple sketch of what I believe is happening in the set up.
Also because the angle that I am dealing with is very small, I made the assumption that sin(theta) = 12.9mm/X (where X in this case is the max distance I need from the observer)
Any help would be much appreciated! Thanks
