Mohmmad Maaitah
- 90
- 20
- Homework Statement
- Resolve to components / Determine magnitude of projections
- Relevant Equations
- Dot product
I don't get what is the difference when I am asked to re-solve components and find projections to axes other than the Y and X
I know that the parallelogram works for the first one and the dot product for the second but what's the diffrence!
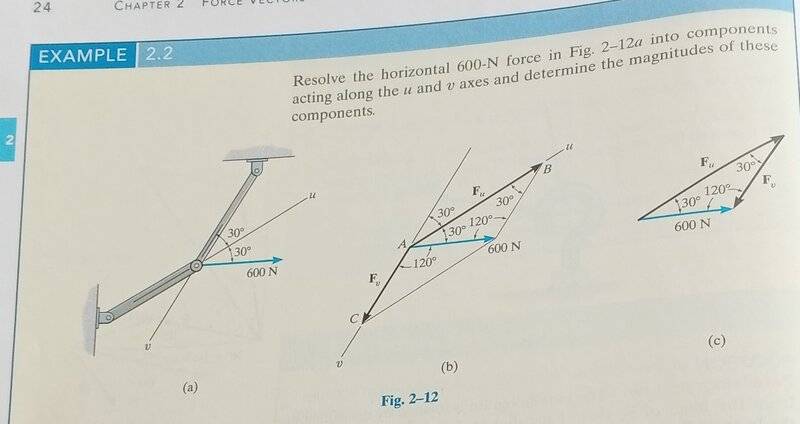
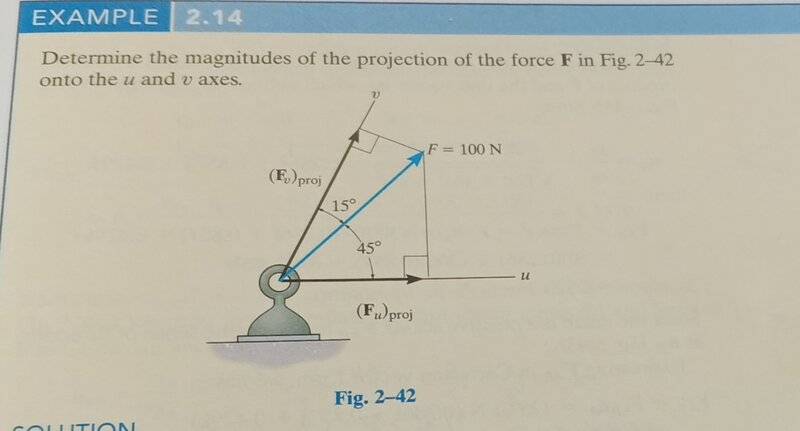
I know that the parallelogram works for the first one and the dot product for the second but what's the diffrence!