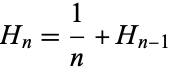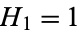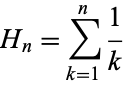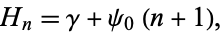alyafey22
Gold Member
MHB
- 1,556
- 2
Prove the following :
$\displaystyle \psi(n)= -\gamma \,+\,\sum^{n-1}_{k=1}\frac{1}{k}$