- #1
- 970
- 670
With some help from another thread, I learned how to solve a simultaneous diophantine approximation involving log(2), log(3), log(5) etc. This method is based on Mathematica's LatticeReduce function. At first, I was quite happy to use it as a black box to work on some hobby math exploration, but now I would like to understand the solution process a bit more precisely.
To this end I set up a toy problem in Mathematica to find a rational approximation to Log[2]. Take the lattice with basis vectors:
( 1, 0 ) and ( Round(10^6 * log(2)) , 10^6 ).
Make a matrix 'a' whose columns are those vectors. Take
But it is not clear to me why this has worked. Here is a diagram showing the original 'a' and the reduced 'b' bases. (One 'a' vector goes off the chart, and one is too small to see, but we'll focus on the reduced bases 'b' which are the blue vectors.
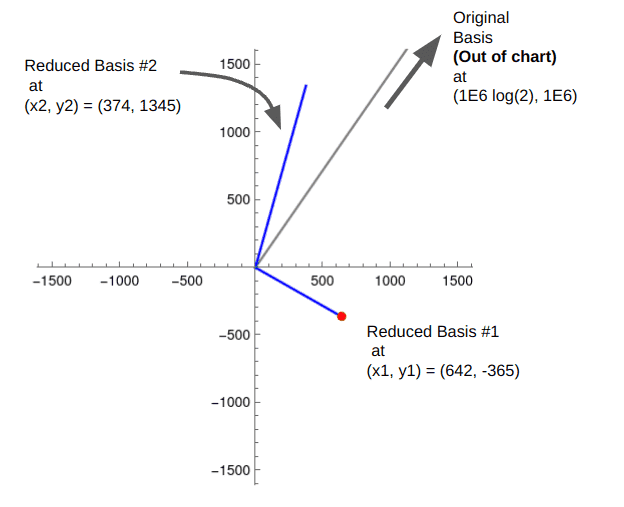
From the fact these blue lines are bases of our original lattice, we can say that there are integers M, N such that
##M x_1 + N x_2 = 642 M + 374 N = Round( 10^6 Log(2) )##.
But how does that make 642*log(2) so close to an integer? (It's giving us 445.004, as mentioned above.)
I suspect that the answer may be something utterly trivial that I am missing, but...
===
Edit: minor correction:
##M x_1 + N x_2 = 642 M + 374 N = Round( 10^6 Log(2) )\LARGE\textbf{ +1}##.
(The +1 has a negligible effect on things FAPP, though).
To this end I set up a toy problem in Mathematica to find a rational approximation to Log[2]. Take the lattice with basis vectors:
( 1, 0 ) and ( Round(10^6 * log(2)) , 10^6 ).
Make a matrix 'a' whose columns are those vectors. Take
b = LatticeReduce[a]. Observe that b(1,1) * log(2) = 642 * log(2) = 445.0004, which is awesome.But it is not clear to me why this has worked. Here is a diagram showing the original 'a' and the reduced 'b' bases. (One 'a' vector goes off the chart, and one is too small to see, but we'll focus on the reduced bases 'b' which are the blue vectors.
From the fact these blue lines are bases of our original lattice, we can say that there are integers M, N such that
##M x_1 + N x_2 = 642 M + 374 N = Round( 10^6 Log(2) )##.
But how does that make 642*log(2) so close to an integer? (It's giving us 445.004, as mentioned above.)
I suspect that the answer may be something utterly trivial that I am missing, but...
===
Edit: minor correction:
##M x_1 + N x_2 = 642 M + 374 N = Round( 10^6 Log(2) )\LARGE\textbf{ +1}##.
(The +1 has a negligible effect on things FAPP, though).
Last edited: