vcsharp2003
- 913
- 179
- Homework Statement
- When an electric dipole is placed in a uniform electric field of ##\vec E## as shown in second diagram below, then does the non-uniform electric field due to the dipole superimpose with the uniform electric field to create a net non-uniform electric field?
- Relevant Equations
- ##\vec E_{net} = \vec E_1 + \vec E_2 + \vec E_3 + ...##, which is the principle of superimposition of electric fields at a point
My understanding is that the uniform electric field ##\vec E## cannot be the net electric field since the dipole creates its own electric field as shown in first diagram below, which must superimpose with the uniform electric field. So, yes, the uniform electric field ##\vec E## around the dipole gets altered to a non-uniform electric field due to the principle of superimposition of electric fields.
Yet, and this gets confusing, when we are determining torque on the dipole as in second diagram, we are calculating the force on each charge as if only the uniform electric ##\vec E## exists without any modification/superimposition. So according to me, the force on each charge should not be just ##qE##, but the vector sum of the forces due to the other charge and ##qE##.
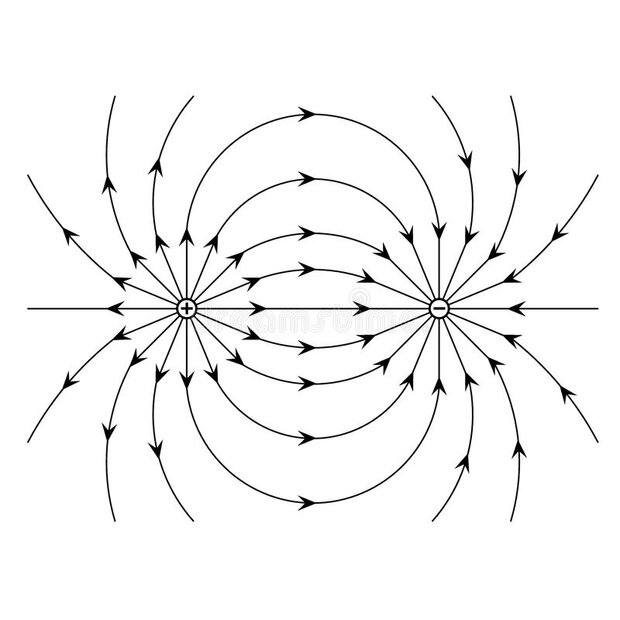
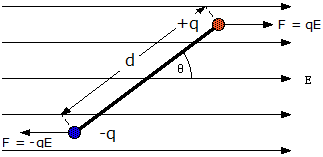
Yet, and this gets confusing, when we are determining torque on the dipole as in second diagram, we are calculating the force on each charge as if only the uniform electric ##\vec E## exists without any modification/superimposition. So according to me, the force on each charge should not be just ##qE##, but the vector sum of the forces due to the other charge and ##qE##.