Discharging a capacitor -- Calculate the current as a function of time

[Lambda96]

Homework Statement

Calculate the current as a function of time when discharging the capacitor

Relevant Equations

none

Hi,

I am not sure if I have calculated the task b correctly.

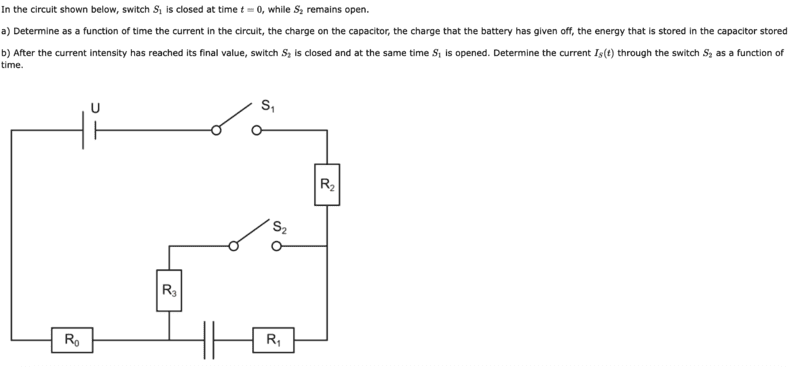
I always interpret an open switch as an infinitely large resistor, which is why no current is flowing through this "resistor". So there is no current in the red circle, as it was the case in task part a, but only in the blue circle.

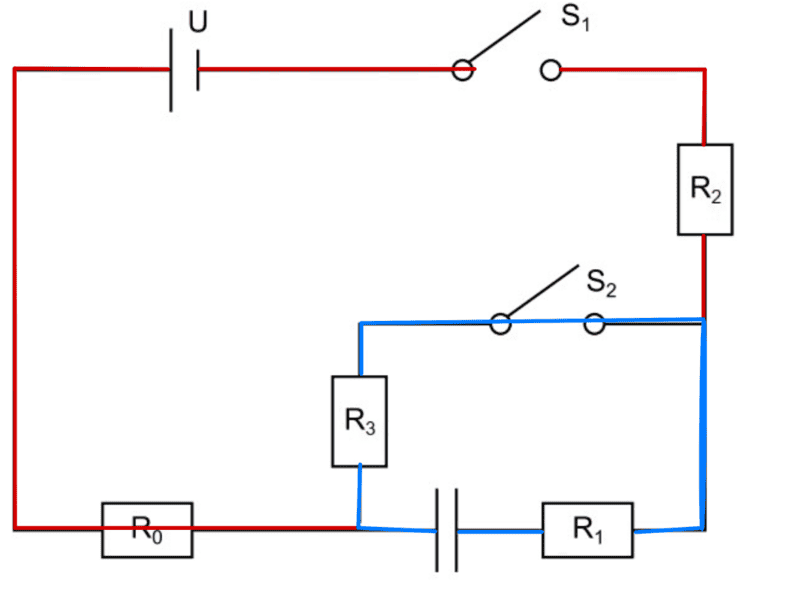
Since the resistors are connected in series, I combined them into one, so $R_g=R_1+R_3$ Then I set up Kirchhoff's rules $\frac{q}{C}=-R_g I$ after that I rewrote the current as follows $\frac{dq}{dt}$ and put it into the equation $\frac{q}{C}=-R_g \frac{dq}{dt}$ and rewrote it as follows and integrated it afterwards.

$$-\frac{1}{R_g C}dt=\frac{1}{q}dq$$
$$ \int_{0}^{t} -\frac{1}{R_g C}dt= \int_{Q_0}^{Q} \frac{1}{q} dq $$
$$-\frac{t}{R_g C}=\ln(\frac{Q}{Q_0})$$
Solve the equation for Q: $Q=Q_0e^{-\frac{t}{R_g C}}$

To get the current now, I simply derived the equation for the charge with respect to time.

$$I(s)=\frac{dQ}{dt}=-\frac{Q_0}{R_g C}e^{-\frac{t}{R_g C}}$$

 

[kuruman]

This would be correct if you have calculated $Q_0$ correctly from part (a).

What does the negative sign in front of the current mean? Is the direction of the current clockwise or counterclockwise?

 

[Lambda96]

Thanks kuruman for looking over my calculation The minus sign came from the derivative of the function for the charge.

For the charge $Q$ I got the following in task a $Q(t)=\epsilon C(1-e^{-\frac{t}{R_g C}})$

$Q_0$ would then be reached at time $T$, so $Q_0(T)=\epsilon C(1-e^{-\frac{T}{R_g C}})$

$\epsilon$ is the voltage of the battery

But if I read the circuit diagram correctly, when charging the capacitor, the left side of the capacitor would be positive and the right side negative. If now the switch $S_1$ is closed and $S_2$ is opened, the positive charges would move to the negative charges, whereby the current would move clockwise and should then be positive, or have I misunderstood the plan and the distribution of the charges on the capacitor?

 

[nasu]

The signs of the current or charge are not really relevant for what the question asks. And there is no absolute rule for taking the current positive or negative. Clockwise does not mean positive unless you choose to be so.