- #1
Jerome1
- 17
- 0
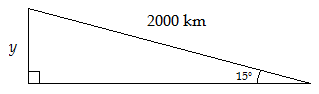
Banjul is approximately 2000 km from Accra. The bearing of Banjul from Accra is 295°. How far north of Accra is Banjul
please give me a clue on how to do this
please give me a clue on how to do this