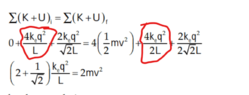member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this problem,

Is the length vector into or out of the page and how do you tell?
EDIT: Why must we use conservation of energy for this problem? I tried solving it like this:
##IdB\sin90 = ma ##
##IdB = ma ##
##v_f = (2aL)^{1/2} ##
##v_f = (\frac {2dIBL} {m})^{1/2} ##
Which is incorrect according to solutions:
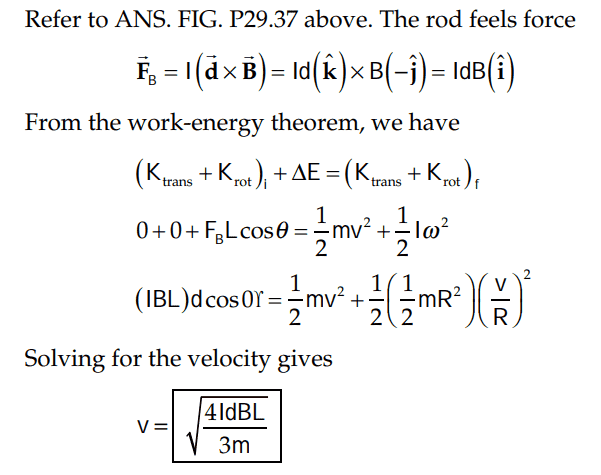
Many thanks!
Is the length vector into or out of the page and how do you tell?
EDIT: Why must we use conservation of energy for this problem? I tried solving it like this:
##IdB\sin90 = ma ##
##IdB = ma ##
##v_f = (2aL)^{1/2} ##
##v_f = (\frac {2dIBL} {m})^{1/2} ##
Which is incorrect according to solutions:
Many thanks!
Last edited by a moderator: