- #1
maistral
- 240
- 17
Hi. I have this PDE that governs an L x L plate (similar to the Poisson equation, it seems)
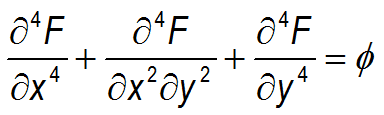
with boundary conditions F = 0 and F" = 0 along the edges. I have successfully solved the problem by setting up an equality W = ∇2F then I solved the two PDEs simultaneously:
W = ∇2F (boundary condition F = 0 along the edges)
φ = ∇2W (boundary condition W = 0 along the edges since W = F").
Simple discretization using second order derivatives followed, then poof. Answer.
What I would like to know is how to solve this without using substitutions (I mean, directly attacking the differentials using fourth-order finite differences). What I did is I took the second order derivative of the second-order finite differences with respect to the same variables (for the non-mixed derivative) and the other variable (for the mixed derivative).
My problem is coming from the boundary conditions. The boundary F = 0 is a no-brainer. The problem is how should I implement the second order boundary condition F" = 0. Does anyone have an idea on how to execute this properly?
What I did is that I tried using the second order three-point formula for the second derivative using double the steps then equated it to zero, then applied the resulting formula to the ghost points formed outside the boundary. ie.
(F(x+2Δx,y) - 2F(x,y) + F(x-2Δx,y)) / (2Δx)2 = 0 say, for points beside the right border then I solved for the ghost point F(x+2Δx,y). I applied the same to the points beside the top, bottom, and left borders.
And, this happened:
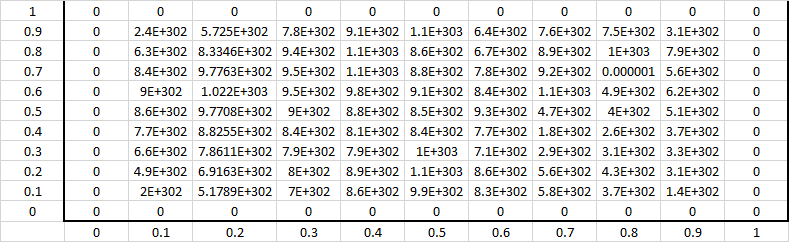




How should I implement the second order condition? I hope for any kind and generous response. Thanks!
with boundary conditions F = 0 and F" = 0 along the edges. I have successfully solved the problem by setting up an equality W = ∇2F then I solved the two PDEs simultaneously:
W = ∇2F (boundary condition F = 0 along the edges)
φ = ∇2W (boundary condition W = 0 along the edges since W = F").
Simple discretization using second order derivatives followed, then poof. Answer.
What I would like to know is how to solve this without using substitutions (I mean, directly attacking the differentials using fourth-order finite differences). What I did is I took the second order derivative of the second-order finite differences with respect to the same variables (for the non-mixed derivative) and the other variable (for the mixed derivative).
My problem is coming from the boundary conditions. The boundary F = 0 is a no-brainer. The problem is how should I implement the second order boundary condition F" = 0. Does anyone have an idea on how to execute this properly?
What I did is that I tried using the second order three-point formula for the second derivative using double the steps then equated it to zero, then applied the resulting formula to the ghost points formed outside the boundary. ie.
(F(x+2Δx,y) - 2F(x,y) + F(x-2Δx,y)) / (2Δx)2 = 0 say, for points beside the right border then I solved for the ghost point F(x+2Δx,y). I applied the same to the points beside the top, bottom, and left borders.
And, this happened:




How should I implement the second order condition? I hope for any kind and generous response. Thanks!