Discussing Interior Schwarzschild Proper Lengths & Gaussian Curvature

[D.S.Beyer]

TL;DR Summary

Does the Gaussian curvature (k) of the interior solution also have the property that distances measured on it match distances in the Schwarzchild metric (like the w definition embedment)?

I'd love have a little discussion about the Interior Schwarzschild Solution.

Here's a diagram I slapped together to illustrate the key points. (I assume everyone reading this familiar with embedding diagrams, and using an axis to 'project' a value, in this case the spatial z-axis is replaced by w. The top left tiny diagrams are the summary of this information. Below them is the visualization of the interior Schwarzschild Solution, taken directly from wikipedia. And to the right is just a zoomed in portion of that diagram with some of the critical information noted)

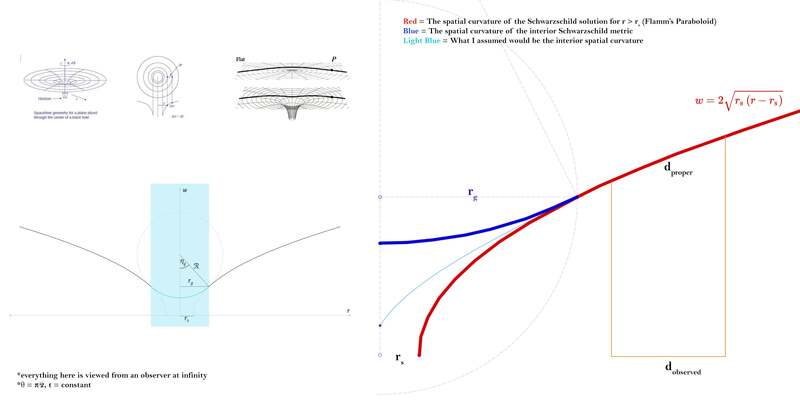
So wikipedia has both Flamm's Paraboloid, and the Interior Solution visualizations stated as "spatial curvature visualizations". My question is, what is happening as you approach the center in regard to the Proper Length (relative to an observer at infinity).

If these are proper lengths...ie "This surface (of Flamm's Paraboloid) has the property that distances measured within it match distances in the Schwarzschild metric" -wikipedia

The interior solution creates a curve that slopes 'up' and become momentarily horizontal in the dead center.

Using the logic of Flamm's Paraboloid, then that means that at the center of the body, the proper length is equal to an observer at infinity's measured length. dp = do . (well...not exactly though, since it will always have a tiny amount of the Gaussian curvature (K). But maybe you could say that the derivative of K at a point at the center of the body of mass is equal to the derivative of a point at infinity.)

That does not jive with me. But if it's true... I think it's wild.

Questions :
Does the Gaussian curvature (K) of the interior solution also have the property that distances measured on it match distances in the Schwarzschild metric (like the w definition embedment)?

Can anyone show me a map of geodesics going through an SSSPF?

Thoughts?

 

[Ibix]

I think you are misinterpreting the embedding diagram. In particular, the quantity you've marked $d_{observed}$ is not observed by anybody. The horizontal distance between two points on your section of the embedding is just the coordinate difference, $\Delta r$, between them in Schwarzschild coordinates. $\Delta r$ is not a quantity you will often see because it's physically meaningless. The only physically relevant distance is the length of the curve along the surface.

The point about Flamm's paraboloid (and your interior version) is that there is a relationship between radial and tangential measured distances, and in Schwarzschild spacetime's static spatial slices that is not Euclidean. You can always draw a circle of circumference $C$ centered on your planet, and hence define a quantity $r=C/2\pi$ that uniquely identifies each circle. Now draw a second circle with circumference $C+dC$ and you get a new $r+dr$. Independently, we can ask what is the distance between those two circles. The answer is not $dr$ - it's slightly larger. And that's all your embedding shows - that $dr^2+dz^2>dr^2$ (in fact it's carefully chosen so that $dr^2+dz^2=g_{rr}dr^2$). It doesn't tell you anything about proper lengths or "lengths measured at infinity" or anything. In fact, if you want to make a remote measurement of length you're going to have to explain how you intend to do that.

As for the interior solution flattening out at the center, of course it does. A non-differentiable curve such as your pale blue one would be very surprising for any reasonable definition of "space". All this shows is that as the circumference, $C$, of your circles goes to zero the quantity $r=C/2\pi$ must get close to the physically measured distance across the diameter of the circle. That is to say that over small regions space must be well approximated by Euclidean space, which is just the spatial part of the equivalence principle. Again, it just says something about the relationship between radial and tangential distances in this metric, and nothing about distances measured remotely.

 

[D.S.Beyer]

Okay this is making more sense. I'm beginning to see some of my weird assumptions in here.

I think the thing that is giving me trouble is the 're-embedment' of the lengths on the curve, back onto the $(r,\varphi)$ plane. This produces these varying $r$ values, which are not actual lengths (as you have said). So, I think I understand why $\Delta r$ is not really a meaningful length.

I assumed that these 'squished' lengths were essentially the responsible factor for an observed 'length contraction' from afar. Which, to me, made sense as the $r$ values are contracted in the direction of gravitational acceleration.

I assumed, loosely, the idea that $\Delta r$ is better defined as something like, a $\Delta \varphi_o$ angle, from the observer (attempting to make $\Delta r$ a strictly visual phenomena). I assumed that the basis coordinate system is Minkowski flat spacetime, and an observer in such flat spacetime, at a distance (infinity), was the view point for this. Thus achieving an extrinsic view of the curvature. (Thinking more closely about this assumption I see what you mean about needing an explanation about how this measurement is taken. First step might be translating the spherical coords of Schwarzschild to Euclidean to even consider an observer making a $\Delta \varphi_o$ measurement. Among other things. It's a mess... I'll need to think more about this distance measurement.)

In short, the basis of my question rested on the assumption that the 'squished' $r$ values were a visible phenomena from an outside observer. Which is why it didn't make sense to me, that an observer somehow seeing the center of a planet, would see these squished values return to normal.

Let me think on this a bit and get back with an attempt at a distant observer measurement.

Thank you for your help.