Amaelle
- 309
- 54
- Homework Statement
- studying the convergence of a serie (look at the image)
- Relevant Equations
- geometric serie, convergence
Good day
I want to study the connvergence of this serie
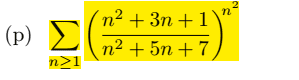
I already have the solution but I want to discuss my approach and get your opinion about it
it s clear that n^2+5n+7>n^2+3n+1 so 0<(n^2+3n+1)/(n^2+5n+7)<1 so we can consider this as a geometric serie that converge?
many thanks in advance
I want to study the connvergence of this serie
I already have the solution but I want to discuss my approach and get your opinion about it
it s clear that n^2+5n+7>n^2+3n+1 so 0<(n^2+3n+1)/(n^2+5n+7)<1 so we can consider this as a geometric serie that converge?
many thanks in advance
Last edited by a moderator: