- #1
Crosshash
- 50
- 0
I'm trying to get my head around what this means exactly. I've plotted the graph to help verse me with the functions that I've derived.
From the free electron model, the wavefunctions are treated as planewaves of the form
[tex]\psi_\mathbf{k}(\mathbf{r}) = e^{i\mathbf{k}\cdot\mathbf{r}} [/tex]
Due to the lattice being periodic, the wavefunction needs to be periodic and this occurs for values of [tex]k_{x,y,z}[/tex] which are of the form
[tex]
k_{x,y,z} = \frac{2n\pi}{a}
[/tex]
When you solve the Schrodinger equation with this wavefunction, the energy eigenvalues are of the form
[tex]E = \frac{\hbar^2 k^2}{2m}[/tex]
which I've plotted as a dispersion relation to give:
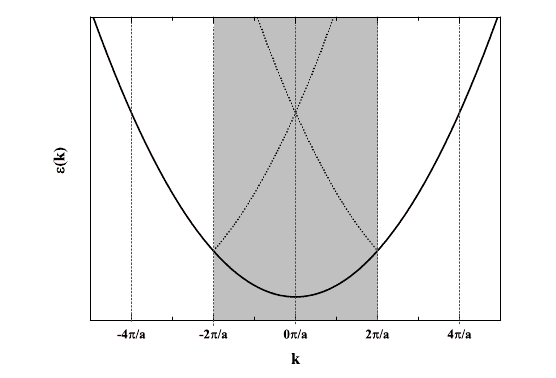
Here's where I'm trying to wrap my head around this. What exactly are we looking at here? Obviously, this is in reciprocal space. n is the quantum number but is it also the brillouin zone index? For n=1, two electrons can occupy that band, does that mean they're restricted to the first brillouin zone? For n=2, are they restricted to the second brillouin zone? Why do so many texts plot the dotted lines the way I've done it (inside the first brillouin zone). What consequence is this?
Thank you
[edit] just to add, I'm working through chapter 6 of Kittel.
From the free electron model, the wavefunctions are treated as planewaves of the form
[tex]\psi_\mathbf{k}(\mathbf{r}) = e^{i\mathbf{k}\cdot\mathbf{r}} [/tex]
Due to the lattice being periodic, the wavefunction needs to be periodic and this occurs for values of [tex]k_{x,y,z}[/tex] which are of the form
[tex]
k_{x,y,z} = \frac{2n\pi}{a}
[/tex]
When you solve the Schrodinger equation with this wavefunction, the energy eigenvalues are of the form
[tex]E = \frac{\hbar^2 k^2}{2m}[/tex]
which I've plotted as a dispersion relation to give:
Here's where I'm trying to wrap my head around this. What exactly are we looking at here? Obviously, this is in reciprocal space. n is the quantum number but is it also the brillouin zone index? For n=1, two electrons can occupy that band, does that mean they're restricted to the first brillouin zone? For n=2, are they restricted to the second brillouin zone? Why do so many texts plot the dotted lines the way I've done it (inside the first brillouin zone). What consequence is this?
Thank you
[edit] just to add, I'm working through chapter 6 of Kittel.