Displacements in a system of two masses connected by three springs

[Istiak]

Homework Statement

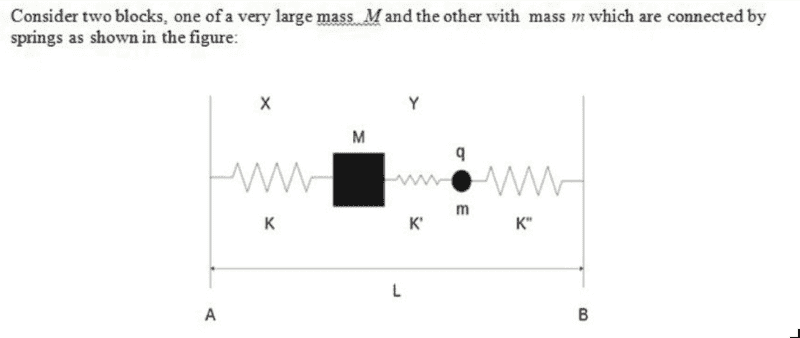
What is the equilibrium values of X and Y (denoted as X0 and Y0 respectively) where X and Y are the displacements of the masses M and m respectively (see figure)?

Relevant Equations

F=qE

Figure :

Option of question :

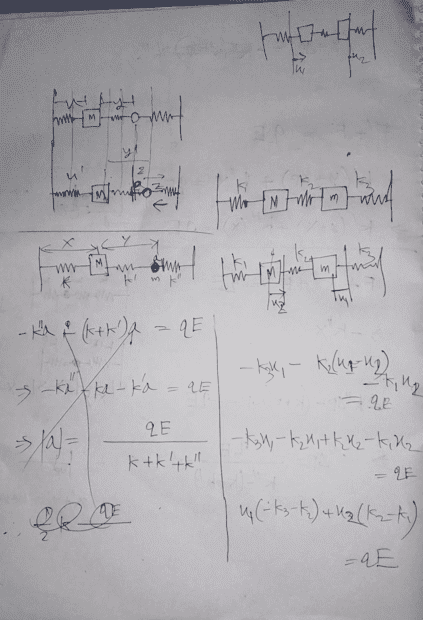
Solution attempt :

 

[willem2]

The formula F = qE is valid for a force F, a spring constant q and an extension of the spring E In general. They are not used in this problem.
You only need X, Y, L and the spring constants K, K' and K''.
The first 3 answers are wrong for this reason, as is your computation.
You need to use equilibrium of of forces for the M and m masses.
Writing down the equations for equilibrium of forces should be pretty simple, there's no need to consider more than 2 springs and 1 mass at the same time.

 

[haruspex]

The formula F = qE is valid for a force F, a spring constant q and an extension of the spring E In general. They are not used in this problem.
You only need X, Y, L and the spring constants K, K' and K''.
The first 3 answers are wrong for this reason, as is your computation.
You need to use equilibrium of of forces for the M and m masses.
Writing down the equations for equilibrium of forces should be pretty simple, there's no need to consider more than 2 springs and 1 mass at the same time.

The problem made no sense to me. Displacements from what? Usually one refers to displacements as being from equilibrium, making the answer X=Y=0.
Then I noticed the q in the diagram. Looks like E is supposed to be an applied electric field, not shown, and q is a charge on m. That would create a new equilibrium, displaced from the fieldless equilibrium.

This still leaves it a bit unclear how X and Y are defined. They are described as displacements of the masses, but in the diagram they appear associated with the spring lengths.
Interpreting them as increases in spring lengths I get one of the given answers. @Istiakshovon, you seem to have trusted the text and taken them as displacements of the masses. But you have not completed the calculation. You got two equations with two unknowns; now you need to solve them.

 

[SammyS]

OP has posted a question with the same figure in the thread:
https://www.physicsforums.com/threads/find-the-electric-field.1004459/
https://www.physicsforums.com/threads/find-the-electric-field.1004459/

Posts 35, 37, and 38 in that thread, come close to making sense of defining X and Y .

Good luck with that.

 

[kuruman]

It seems to me I've seen this kind of movie before here
https://www.physicsforums.com/threads/find-the-electric-field.1004459/page-2#post-6508142.
This one has a slightly different script, but it suffers from the same symptoms: X and Y are ill-defined. We are told they are "displacements". As we all know, displacements are differences between positions. We are not told whether the displacements X and Y are relative to the same origin, e.g. point A, or whether each of them has its own origin and what that is.

As with the previous movie, we can assume that the displacements of the masses are relative to their equilibrium positions when the external electric field is OFF. Under this assumption, there is a correct answer among the five. It can be reached by two approaches: (a) use free body diagrams to derive the expressions for X and Y and (b) use logic to eliminate four of the choices that cannot be correct. Of course, eliminating four choices does not guarantee that the remaining fifth choice is correct, not in this movie. Thus, it becomes important to get the answer in two different ways to reinforce one's belief that the problem has been solved correctly.

To @Istiakshovon: Your equations don't make sense. It seems that you are trying to balance forces, but I see no force expressions. To get a force, you need to multiply a spring constant by a displacement. I see no such terms on the right-hand side of your attempt at a solution. Please try harder.

I thought I had sent this, but I hadn't. Here is it is anyway. It echoes some of what has already been said.

 

[Steve4Physics]

This may be one of several questions about the same system.

Apart from the inadequate definitions of X and Y, I suspect that @Istiakshovon hasn't included all the necessary contextual information. For example the question doesn't even mention 'electric field'. Which means a lot of guesswork is needed.

 

[haruspex]

you need to multiply a spring constant by a displacement. I see no such terms on the right-hand side of your attempt at a solution

You may be misreading the handwriting. There are terms like $k_2x_1$, but the x's look more like k's.

 

[kuruman]

You may be misreading the handwriting. There are terms like $k_2x_1$, but the x's look more like k's.

Ah, yes. That's what it is. Thanks.

 

[Istiak]

This may be one of several questions about the same system.

Apart from the inadequate definitions of X and Y, I suspect that @Istiakshovon hasn't included all the necessary contextual information. For example the question doesn't even mention 'electric field'. Which means a lot of guesswork is needed.

I said in my last thread that I gave all of information. I am saying the same thing for the question also. Actually, this question was for Physics Olympiad (I think everyone knows what it is). They write question as hard as possible. Even, I didn't know that did the question say to find displacement. Those options was looking like finding displacement that's why I just said that. Even, the main examiner told yes either.

 

[haruspex]

I said in my last thread that I gave all of information. I am saying the same thing for the question also. Actually, this question was for Physics Olympiad (I think everyone knows what it is). They write question as hard as possible. Even, I didn't know that did the question say to find displacement. Those options was looking like finding displacement that's why I just said that. Even, the main examiner told yes either.

Can you provide a link to the question paper? I trawled through some past papers at the Bangladesh Physics Olympiad site but couldn’t find it.

 

[Istiak]

Can you provide a link to the question paper? I trawled through some past papers at the Bangladesh Physics Olympiad site but couldn’t find it.

Sorry! The exam was taken in online-bdpho.azurewebsites.net . They don't submit those question papers very fast. Maybe, they uploads paper in 8-9 months. Even, I am not sure they submits Regional and, National papers or not. In [this page](https://bdpho.org/index.php/site/past_question_paper.html) they submitted lot of question papers. I think most of them are International Question papers ~ I am not sure cause, I haven't get to Apho (Asian) and, National also.

 

[Steve4Physics]

Sorry! The exam was taken in online-bdpho.azurewebsites.net .

This above link only displays the word 'Working', greyed-out. Nothing else. How did you get the images in Post#1?

 

[Steve4Physics]

I said in my last thread that I gave all of information.

This is a different (though related) question to the one in your last thread. You can't rely on people having read (or even being aware of) what was said in other threads. You will get the best help if questions are complete/self-contained.

 

[Istiak]

This is a different (though related) question to the one in your last thread. You can't rely on people having read (or even being aware of) what was said in other threads. You will get the best help if questions are complete/self-contained.

I didn't write the question. So, how can I complete it? :(

 

[Istiak]

This is a different (though related) question to the one in your last thread. You can't rely on people having read (or even being aware of) what was said in other threads. You will get the best help if questions are complete/self-contained.

Person who was examiner he had taken screenshot. That page doesn't available anymore.

 

[Steve4Physics]

I didn't write the question. So, how can I complete it? :(

You can't complete a question unless you are provided with the necessary information. It is not your fault if information is missing.

I'd guess the intended question is something like this...

Call the springs (left to right) 1, 2 and 3 with spring constants k₁, k₂ and k₃ respectively.

[spring 1]M[spring 2][m][spring 3] (see original diagram)

With no electric field the springs are at their natural lengths.

When electric field E is applied, the charge (q) on m causes m to experience a force, qE, to he right. The system reaches a new equilibrium.

M has been displaced right a distance X and m has been displaced right a distance Y.

What are X and Y in terms of k₁, k₂, k₃ q and E?
_________________
Solution

Spring 1 is extended a distance X so its tension is k₁X.
Spring 2 is extended a distance Y-X so its tension is k₂(Y-X).
Spring 3 is compressed (assuming no buckling) a distance Y so its compression is k₃Y.

Balancing the forces on M gives: k₁X = k₂(Y-X)
Balancing the forces on m gives: k₂(Y-X) + k₃Y = qE

That’s all the physics done. The rest is algebra - the above 2 equations can be solved to find X and Y. I don’t know if the answer matches any of the answers in the answer-list, but you can give it a try.

 

[kuruman]

$\dots$

M has been displaced right a distance X and m has been displaced right a distance Y.

What are X and Y in terms of k₁, k₂, k₃ q and E?
_________________
Solution

Spring 1 is extended a distance X so its tension is k₁X.
Spring 2 is extended a distance Y-X so its tension is k₂(Y-X).
Spring 3 is compressed (assuming no buckling) a distance Y so its compression is k₃Y.

My interpretation differs from yours. I agree with you with the setup of the problem and with your definition for X. However, as far as Y is concerned, I think it is the change in length of the middle spring relative to its own relaxed length. In that case, one would have
Spring 1 is extended a distance X so its tension is k₁X.
Spring 2 is extended a distance Y so its tension is k₂Y.
Spring 3 is compressed (assuming no buckling) a distance (X+Y) so its compression is k₃(X+Y).

With this interpretation, one of the given choices matches the answers obtained by solving the system of two equations and two unknowns. That the other four choices cannot be correct, can be independently verified with a little bit of thought.

Physics Olympiad problems may be made difficult but not by withholding information and requiring the solver to divine what was in the author's mind. That is a task best relegated to a haruspex.