- #1
computerex
- 68
- 0
Hello. Up until this point I have been solving this numerically, by propagating the state vectors and checking for a collision, however that is inefficient, so I would like an analytic solution.
Given lengths r, and d, as well as angle t, is there a way to find length s?
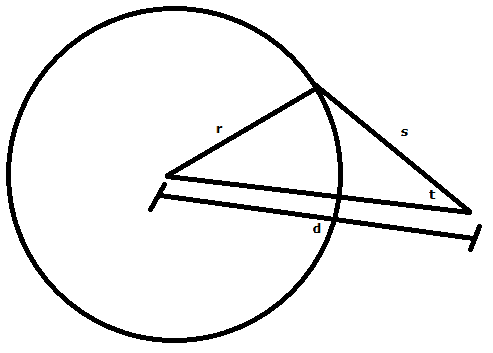
Given lengths r, and d, as well as angle t, is there a way to find length s?