Yankel
- 390
- 0
Hello all,
Below there is a problem:
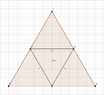
There are five points inside an equilateral triangle of side length 2. Show that at least two of the points are within 1 unit distance from each other.
I have plotted such a triangle using "Geogebra", and attaching the picture.
I know that if I create another equilateral triangle within the original one, I get four triangles. Then, according to the pigeonhole principle, with 5 points (pigeons) and 4 triangle (holes), at least two points will be in the same triangle.
My questions are:
1) What is the geometrical reasoning for claiming that two points within a triangle will have a distance of 1 units max ? I couldn't prove it.
2) What happens if a point in the bigger triangle happens to be on the edge of the inner black triangle? Doesn't it disproof the theory ?
Thank you in advance !
View attachment 7554
Below there is a problem:
There are five points inside an equilateral triangle of side length 2. Show that at least two of the points are within 1 unit distance from each other.
I have plotted such a triangle using "Geogebra", and attaching the picture.
I know that if I create another equilateral triangle within the original one, I get four triangles. Then, according to the pigeonhole principle, with 5 points (pigeons) and 4 triangle (holes), at least two points will be in the same triangle.
My questions are:
1) What is the geometrical reasoning for claiming that two points within a triangle will have a distance of 1 units max ? I couldn't prove it.
2) What happens if a point in the bigger triangle happens to be on the edge of the inner black triangle? Doesn't it disproof the theory ?
Thank you in advance !
View attachment 7554