- #1
Kairos
- 182
- 16
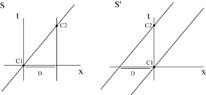
Two planets are immobile one with respect to the other and distant of D. A rocket passes from one to the other at high speed v. Is the distance really traveled by the rocket between these planets D or only D*sqrt(1-(v/c)^2) ?