Slipjoints
- 6
- 1
- Homework Statement
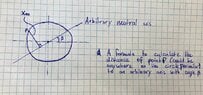
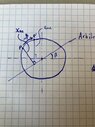
- Formulate an equation for the shortest distance from a point to a line
- Relevant Equations
- Pythagorean Theorem / Thales?
Hi all! In this assignment I have to formulate an equation for the shortest distance from a point on a circle perimeter to an arbitrary axis in a circle with angle theta. I included an image with the sketch. Anyone that can help?