Distance traveled by a ball down a ramp and on a flat path

[avi]

TL;DR Summary

How should the conversation of energy principle be applied to determining the distance that a ball would travel on a flat path if the only thing known is the distance the ball traveled on a flat path and up a ramp where it stopped at the top of the ramp.

Question: A ball is hit with a certain force and it starts with an initial velocity of V m/sec decelerating due to friction along a flat path and then up an inclined ramp coming to stop at the top of the ramp where the ramp becomes flat again (as per diagram A). The total distance traveled along the horizontal direction is R meters, is it correct to say that the additional distance the ball would have traveled (F- R) had there been no ramp as seen in diagram B can be determined by rolling the ball from a stationary position on top of the ramp down the ramp until it stops as seen in diagram C?

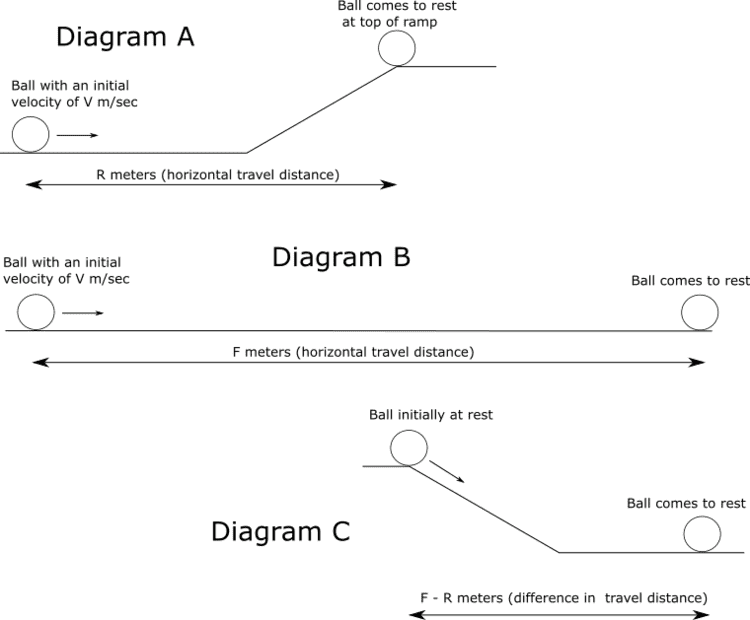
Here are my calculations. As energy is conserved in any closed system, one could argue that in Diagram A, the initial kinetic energy is equal to the potential energy when the ball stops on the top + the loss in energy to friction. So, 0.5mv^2 = mgh + loss1 . For Diagram B, the entire kinetic energy is lost to friction by the time the ball stops, so the equation would be 0.5mv^2 = loss . For Diagram C, as the potential energy is lost to friction, so the equation is mgh = loss2 . From equations of Diagrams A and C, 0.5mv^2 = loss2 + loss1 . As loss1 + loss2 = loss , so one could write equation as 0.5mv^2 = loss, which is the equation for Diagram B. Thus I would argue that it is correct to say that the additional distance the ball would have traveled would be (F- R) had there been no ramp as seen in diagram B.

 

[Baluncore]

Welcome to PF.
When a ball is rolling, it has linear kinetic energy, plus angular kinetic energy.

 

[avi]

Welcome to PF.
When a ball is rolling, it has linear kinetic energy, plus angular kinetic energy.

Thank you, so that would mean the current formula for kinetic energy in the above equations be replaced with the linear + rotational kinetic energy formula, but that would not change the derived results.

 

[f95toli]

Isn't that a trivial result?
If
-the distance the ramp travels without the ramp is F
-the distance it travels with the ramp is R
Then it follows that the difference between the two is F-R....

I am not sure I understand what you are trying to calculate?

 

[avi]

Isn't that a trivial result?
If
-the distance the ramp travels without the ramp is F
-the distance it travels with the ramp is R
Then it follows that the difference between the two is F-R....

I am not sure I understand what you are trying to calculate?

It is not a trivial result. Let me use your words to rephrase the question.
If
-the distance the ramp ball travels without the ramp is F
-the distance it travels with the ramp is R
Then it follows that the difference between the two is F-R....However, if F is unknown, can one just roll the ball down the ramp and when it stops, measure that distance horizontally from the start position and assume that would be equal to F-R?

 

[Baluncore]

When a ball rolls down a ramp with (rolling resistance) friction, is the friction the same as when the ball rolls up the ramp?
As the ball crosses the bottom (or the top) of a ramp, the vertical velocity changes. To change the velocity, there must be acceleration and therefore an additional force. How does that change the friction?

 

[nasu]

How do you know that loss1+loss2=loss? What formulas do you use for these terms?

 

[avi]

When a ball rolls down a ramp with (rolling resistance) friction, is the friction the same as when the ball rolls up the ramp?
As the ball crosses the bottom (or the top) of a ramp, the vertical velocity changes. To change the velocity, there must be acceleration and therefore an additional force. How does that change the friction?

The friction may be slightly greater only for an instant during which the ball transitions to going up the slope. The additional force you are talking about is just the higher normal force for that instant induced by the slope the ball encounters. Also the total frictional loss on the up-slope and the down-slope will be the same as over the corresponding distance traversed on a flat path in diagram B due to the lower normal forces and more distance traveled on the slopes.

 

[avi]

How do you know that loss1+loss2=loss? What formulas do you use for these terms?

Well, both the LHS and RHS are equal to mgh per the mentioned equations, so that is pretty straightforward.

 

[jbriggs444]

The friction may be slightly greater only for an instant during which the ball transitions to going up the slope.

This is an insufficiently cautious assumption. Rather than "slightly greater", the correct phrase is "infinitely greater". @haruspex did an insight on this recently.

The idea is that with an instantaneous change of direction there is an associated infinite normal force, albeit resulting in a finite impulse. Associated with this infinite normal force is the potential for an infinite frictional force. Again, the frictional impulse will be finite.

Let me try to find that insight and add a reference... here it is. Lots of subtleties to think about.

 

[avi]

This is an insufficiently cautious assumption. Rather than "slightly greater", the correct phrase is "infinitely greater". @haruspex did an insight on this recently.

The idea is that with an instantaneous change of direction there is an associated infinite normal force, albeit a finite impulse. Associated with this infinite normal force is the potential for an infinite frictional force. Again, the frictional impulse will be finite.

Let me try to find that insight and add a reference... here it is

Look forward to that insight, but if you say infinitely greater normal force that means the ball would stop as soon as it encounters the slope due to the infinitely greater frictional loss (read complete loss of energy to friction), which is not the case. So it has to be finite, but even so not sure if the loss to friction to that would change the amount of loss to friction over the span of the slope as compared to a flat path.
Also, how can you have infinite force but finite impulse, as anything multiplied with infinite is infinite?

 

[jbriggs444]

Look forward to that insight, but if you say infinitely greater normal force that means the ball would stop as soon as it encounters the slope due to the infinitely greater frictional loss
[...]
anything multiplied with infinite is infinite?

Not so. When you multiply an infinite force by a zero duration you get an undefined impulse. In order to figure out what really happens, you have to use a different calculation. A good start is to multiply the normal impulse by the coefficient of friction to get the frictional impulse.

One could justify this approach by taking the limit of a more realistic interaction as the rigidity and elasticity of the components each approach the ideals of perfect rigidity and perfect elasticity more and more closely.

 

[haruspex]

Question: A ball is hit with a certain force

First up, you don't hit with a force; you hit with an impulse. Secondly, this implies it is not initially rotating…

decelerating due to friction along a flat path

… so there will indeed be friction as it transitions to rolling. There may also be rolling resistance, but that is not mentioned.
We are not told whether it achieves rolling before encountering the ramp, nor whether the coefficient of static friction exceeds the tangent of the ramp angle.

All that makes me suspect the question should have been "A block is set sliding…" and stated $\mu_s<\tan(\theta)$. The ramp transition would have to be made gentler to avoid impacts.
Alternatively, it could be a ball set rolling, unlimited static friction, gentle transitions, rolling resistance coefficient $<\tan(\theta)$.

Either way,

• I note it only refers to horizontal distances, but the distances on the slopes will matter.
• Both kinetic friction force and rolling resistance are proportional to the normal force, which will be less on the slopes.

Maybe those two cancel. Haven’t checked.